Πολλοί μαθητές γυμνασίου ξεχνούν πώς να κάνουν long division. Οι υπολογιστές, οι αριθμομηχανές, τα κινητά τηλέφωνα και άλλες συσκευές έχουν ενσωματωθεί τόσο στενά στη ζωή μας που μερικές φορές οι στοιχειώδεις μαθηματικές πράξεις οδηγούν σε λήθαργο. Και πώς τα κατάφεραν οι άνθρωποι χωρίς όλα αυτά τα οφέλη πριν από μερικές δεκαετίες; Πρώτα πρέπει να θυμάστε τις κύριες μαθηματικές έννοιες που χρειάζονται για τη διαίρεση. Άρα, το μέρισμα είναι ο αριθμός που θα διαιρεθεί. Ο διαιρέτης είναι ο αριθμός με τον οποίο πρέπει να διαιρεθεί. Αυτό που συμβαίνει ως αποτέλεσμα ονομάζεται ιδιωτικό. Για τη διαίρεση σε μια γραμμή, χρησιμοποιείται ένα σύμβολο παρόμοιο με άνω και κάτω τελεία - ":", και όταν χωρίζεται σε στήλη, χρησιμοποιείται το εικονίδιο "∟", ονομάζεται επίσης γωνία με άλλο τρόπο.
Αξίζει επίσης να υπενθυμίσουμε ότι οποιαδήποτε διαίρεση μπορεί να ελεγχθεί με πολλαπλασιασμό. Για να ελέγξετε το αποτέλεσμα της διαίρεσης, αρκεί να το πολλαπλασιάσετε με έναν διαιρέτη, ως αποτέλεσμα, θα πρέπει να λάβετε έναν αριθμό που αντιστοιχεί στο μέρισμα (a: b \u003d c, επομένως, c * b \u003d a). Τώρα για το τι είναι δεκαδικό κλάσμα. Ένα δεκαδικό προκύπτει διαιρώντας μια μονάδα με το 0,0, το 1000 κ.λπ. Η εγγραφή αυτών των αριθμών και των μαθηματικών πράξεων με αυτούς είναι ακριβώς η ίδια όπως και με τους ακέραιους. Κατά τη διαίρεση δεκαδικών ψηφίων, δεν χρειάζεται να θυμάστε πού βρίσκεται ο παρονομαστής. Όλα γίνονται τόσο ξεκάθαρα όταν γράφετε έναν αριθμό. Πρώτα γράφεται ένας ακέραιος αριθμός και μετά την υποδιαστολή γράφονται τα δέκατα, τα εκατοστά, τα χιλιοστά του. Το πρώτο ψηφίο μετά την υποδιαστολή αντιστοιχεί σε δεκάδες, το δεύτερο σε εκατοντάδες, το τρίτο σε χιλιάδες κ.ο.κ.
Κάθε μαθητής πρέπει να ξέρει πώς να διαιρεί τα δεκαδικά ψηφία. Αν και το μέρισμα και ο διαιρέτης πολλαπλασιαστούν με τον ίδιο αριθμό, τότε η απάντηση, δηλαδή το πηλίκο, δεν θα αλλάξει. Εάν το δεκαδικό κλάσμα πολλαπλασιαστεί με 0,0, 1000 κ.λπ., τότε το κόμμα μετά τον ακέραιο αριθμό θα αλλάξει τη θέση του - θα μετακινηθεί προς τα δεξιά με τόσα ψηφία όσα μηδενικά υπάρχουν στον αριθμό με τον οποίο πολλαπλασιάστηκε. Για παράδειγμα, όταν πολλαπλασιάζουμε ένα δεκαδικό με 10, η υποδιαστολή θα μετακινήσει έναν αριθμό προς τα δεξιά. 2,9: 6,7 - πολλαπλασιάζουμε και τον διαιρέτη και τον διαιρετέο με 100, παίρνουμε 6,9: 3687. Είναι καλύτερο να πολλαπλασιάσουμε έτσι ώστε όταν πολλαπλασιάζεται με αυτόν, τουλάχιστον ένας αριθμός (διαιρέτης ή μέρισμα) να μην έχει ψηφία μετά την υποδιαστολή , δηλαδή να γίνει τουλάχιστον ένας αριθμός ακέραιος. Μερικά ακόμη παραδείγματα αναδίπλωσης κόμματος μετά από έναν ακέραιο αριθμό: 9.2: 1.5 = 2492: 2.5; 5,4:4,8 = 5344:74598.
Προσοχή, το δεκαδικό κλάσμα δεν θα αλλάξει την τιμή του αν του εκχωρηθούν μηδενικά στα δεξιά, για παράδειγμα 3,8 = 3,0. Επίσης, η τιμή του κλάσματος δεν θα αλλάξει εάν τα μηδενικά στο τέλος του αριθμού αφαιρεθούν από αυτό στα δεξιά: 3,0 = 3,3. Ωστόσο, τα μηδενικά στη μέση του αριθμού δεν μπορούν να αφαιρεθούν - 3.3. Πώς να διαιρέσετε ένα δεκαδικό κλάσμα με έναν φυσικό αριθμό σε μια στήλη; Για να διαιρέσετε ένα δεκαδικό κλάσμα σε έναν φυσικό αριθμό σε μια στήλη, πρέπει να κάνετε την κατάλληλη καταχώρηση με μια γωνία, διαίρεση. Σε ένα ιδιωτικό κόμμα, πρέπει να το βάλετε όταν τελειώσει η διαίρεση ενός ακέραιου. Για παράδειγμα, 5,4|2 14 7,2 18 18 0 4 4 0 Εάν το πρώτο ψηφίο στο μέρισμα είναι μικρότερο από το διαιρέτη, τότε χρησιμοποιούνται τα επόμενα ψηφία μέχρι να είναι δυνατή η πρώτη ενέργεια.
ΣΕ αυτή η υπόθεση, το πρώτο ψηφίο του μερίσματος είναι 1, δεν μπορεί να διαιρεθεί με το 2, επομένως, δύο ψηφία 1 και 5 χρησιμοποιούνται ταυτόχρονα για τη διαίρεση: το 15 διαιρείται με το 2 με το υπόλοιπο, προκύπτει στο ιδιωτικό 7 και μένει το 1 Στη συνέχεια χρησιμοποιούμε το επόμενο ψηφίο του μερίσματος - 8. Κατεβαίνουμε στο 1 και διαιρούμε το 18 με 2. Στο πηλίκο σημειώνουμε τον αριθμό 9. Δεν μένει τίποτα στο υπόλοιπο, οπότε γράφουμε 0. Χαμηλώνουμε τον υπόλοιπο αριθμό 4 του μερίσματος προς τα κάτω και διαιρούμε με τον διαιρέτη, δηλαδή με το 2. Στο πηλίκο γράφουμε 2, και το υπόλοιπο είναι πάλι 0. Το αποτέλεσμα μιας τέτοιας διαίρεσης είναι ο αριθμός 7.2. Λέγεται ιδιωτικό. Είναι αρκετά εύκολο να λύσετε το ερώτημα πώς να διαιρέσετε ένα δεκαδικό κλάσμα με ένα δεκαδικό κλάσμα σε μια στήλη, αν γνωρίζετε κάποια κόλπα. Η διαίρεση των δεκαδικών ψηφίων στο κεφάλι σας είναι μερικές φορές αρκετά δύσκολη, επομένως χρησιμοποιείται μεγάλη διαίρεση για να διευκολύνει τη διαδικασία.
Με αυτή τη διαίρεση, ισχύουν όλοι οι ίδιοι κανόνες όπως όταν διαιρούμε ένα δεκαδικό κλάσμα με έναν ακέραιο ή όταν διαιρούμε σε μια συμβολοσειρά. Αριστερά στη γραμμή, γράψτε το μέρισμα, μετά βάλτε το σύμβολο "γωνία" και μετά γράψτε τον διαιρέτη και ξεκινήστε τη διαίρεση. Για να διευκολυνθεί η διαίρεση και η μεταφορά σε ένα βολικό μέρος, ένα κόμμα μετά από έναν ακέραιο μπορεί να πολλαπλασιαστεί με δεκάδες, εκατοντάδες ή χιλιάδες. Για παράδειγμα, 9,2: 1,5 \u003d 24920: 125. Προσοχή, και τα δύο κλάσματα πολλαπλασιάζονται με 0,0, 1000. Εάν το μέρισμα πολλαπλασιάστηκε με 10, τότε ο διαιρέτης πολλαπλασιάζεται επίσης με 10. Σε αυτό το παράδειγμα, τόσο το μέρισμα όσο και ο διαιρέτης πολλαπλασιάστηκαν με 100. Στη συνέχεια, ο υπολογισμός εκτελείται με τον ίδιο τρόπο όπως φαίνεται στο παράδειγμα της διαίρεσης δεκαδικό κλάσμα με φυσικό αριθμό. Για να διαιρεθεί με το 0,1; 0,1; 0,1 κ.λπ., είναι απαραίτητο να πολλαπλασιάσουμε και τον διαιρέτη και το μέρισμα με 0,0, 1000.
Αρκετά συχνά, κατά τη διαίρεση σε πηλίκο, δηλαδή στην απάντηση, προκύπτουν άπειρα κλάσματα. Σε αυτήν την περίπτωση, είναι απαραίτητο να στρογγυλοποιήσετε τον αριθμό σε δέκατα, εκατοστά ή χιλιοστά. Σε αυτήν την περίπτωση, ισχύει ο κανόνας, εάν μετά τον αριθμό στον οποίο πρέπει να στρογγυλοποιήσετε η απάντηση είναι μικρότερη ή ίση με 5, τότε η απάντηση στρογγυλοποιείται προς τα κάτω, εάν είναι μεγαλύτερη από 5 - προς τα πάνω. Για παράδειγμα, θέλετε να στρογγυλοποιήσετε το αποτέλεσμα 5,5 στα χιλιοστά. Αυτό σημαίνει ότι η απάντηση μετά την υποδιαστολή πρέπει να τελειώνει με τον αριθμό 6. Μετά το 6 υπάρχει 9, που σημαίνει ότι η απάντηση στρογγυλοποιείται προς τα πάνω και παίρνουμε 5,7. Αλλά αν ήταν απαραίτητο να στρογγυλοποιηθεί η απάντηση 5,5 όχι στα χιλιοστά, αλλά στα δέκατα, τότε η απάντηση θα έμοιαζε με αυτό - 5,2. Σε αυτήν την περίπτωση, το 2 δεν στρογγυλοποιήθηκε επειδή ακολουθείται από το 3 και είναι μικρότερο από το 5.
§ 107. Πρόσθεση δεκαδικών κλασμάτων.Η πρόσθεση δεκαδικών γίνεται με τον ίδιο τρόπο όπως η πρόσθεση ακέραιων αριθμών. Ας το δούμε αυτό με παραδείγματα.
1) 0,132 + 2,354. Ας υπογράψουμε τους όρους ο ένας κάτω από τον άλλο.
Εδώ, από την προσθήκη 2 χιλιοστών με 4 χιλιοστά, προέκυψαν 6 χιλιοστά.
από την προσθήκη 3 εκατοστών με 5 εκατοστά, βγήκαν 8 εκατοστά?
από την πρόσθεση 1 δέκατου με 3 δέκατα -4 δέκατα και
από την προσθήκη 0 ακεραίων με 2 ακέραιους αριθμούς - 2 ακέραιους αριθμούς.
2) 5,065 + 7,83.
Δεν υπάρχουν χιλιοστά στον δεύτερο όρο, επομένως είναι σημαντικό να μην κάνετε λάθη όταν υπογράφετε τους όρους ο ένας κάτω από τον άλλο.
3) 1,2357 + 0,469 + 2,08 + 3,90701.
Εδώ, όταν προσθέτουμε χιλιοστά, παίρνουμε 21 χιλιοστά. γράψαμε 1 κάτω από τα χιλιοστά και 2 προσθέσαμε στα εκατοστά, οπότε στην εκατοστή θέση πήραμε τους ακόλουθους όρους: 2 + 3 + 6 + 8 + 0. αθροιστικά δίνουν 19 εκατοστά, υπογράψαμε 9 κάτω από εκατοστά, και το 1 μετρήθηκε ως δέκατα κ.λπ.
Έτσι, κατά την προσθήκη δεκαδικών κλασμάτων, πρέπει να τηρείται η ακόλουθη σειρά: τα κλάσματα υπογράφονται το ένα κάτω από το άλλο έτσι ώστε σε όλους τους όρους τα ίδια ψηφία να βρίσκονται το ένα κάτω από το άλλο και όλα τα κόμματα να βρίσκονται στην ίδια κάθετη στήλη. δεξιά από τα δεκαδικά ψηφία κάποιων όρων αποδίδουν, τουλάχιστον διανοητικά, τέτοιο αριθμό μηδενικών ώστε όλοι οι όροι μετά την υποδιαστολή να έχουν τον ίδιο αριθμό ψηφίων. Στη συνέχεια, η πρόσθεση εκτελείται με ψηφία, ξεκινώντας από τη δεξιά πλευρά, και στο ποσό που προκύπτει τοποθετείται κόμμα στην ίδια κάθετη στήλη με αυτούς τους όρους.
§ 108. Αφαίρεση δεκαδικών κλασμάτων.
Η αφαίρεση των δεκαδικών γίνεται με τον ίδιο τρόπο όπως η αφαίρεση των ακέραιων αριθμών. Ας το δείξουμε αυτό με παραδείγματα.
1) 9,87 - 7,32. Ας υπογράψουμε το subtrahend κάτω από το minuend έτσι ώστε οι μονάδες του ίδιου ψηφίου να βρίσκονται η μία κάτω από την άλλη:
2) 16.29 - 4.75. Ας υπογράψουμε το subtrahend κάτω από το minuend, όπως στο πρώτο παράδειγμα:
Για να αφαιρέσει κανείς δέκατα, έπρεπε να πάρει μια ολόκληρη μονάδα από το 6 και να τη χωρίσει σε δέκατα.
3) 14.0213-5.350712. Ας υπογράψουμε το υπόβαθρο κάτω από το minuend:

Η αφαίρεση έγινε ως εξής: αφού δεν μπορούμε να αφαιρέσουμε 2 εκατομμυριοστά από το 0, θα πρέπει να αναφερθούμε στο πλησιέστερο ψηφίο στα αριστερά, δηλαδή στα εκατό χιλιοστά, αλλά υπάρχει επίσης μηδέν στη θέση των εκατοστών χιλιάδων, οπότε παίρνουμε 1 δέκα χιλιάδες από 3 δεκαχιλιοστές και το χωρίζουμε σε εκατοντάδες χιλιάδες, παίρνουμε 10 εκατοντάδες χιλιάδες, από τα οποία τα 9 εκατοντάδες χιλιάδες μένουν στην κατηγορία των εκατοντάδων χιλιάδων και το 1 εκατο χιλιοστό συνθλίβεται σε εκατομμυριοστά, παίρνουμε 10 εκατομμυριοστά. Έτσι, στα τρία τελευταία ψηφία, πήραμε: εκατομμυριοστά 10, εκατοντάδες χιλιοστά 9, δέκα χιλιοστά 2. Για μεγαλύτερη σαφήνεια και ευκολία (για να μην ξεχνάμε), αυτοί οι αριθμοί γράφονται πάνω από τα αντίστοιχα κλασματικά ψηφία του μειωμένου. Τώρα μπορούμε να αρχίσουμε να αφαιρούμε. Αφαιρούμε 2 εκατομμυριοστά από τα 10 εκατομμυριοστά, παίρνουμε 8 εκατομμυριοστά. αφαιρούμε το 1 εκατοστό χιλιοστό από το 9 εκατοστό χιλιοστό, παίρνουμε 8 εκατοστό χιλιάδες κ.λπ.
Έτσι, κατά την αφαίρεση των δεκαδικών κλασμάτων, παρατηρείται η ακόλουθη σειρά: το αφαιρούμενο υπογράφεται κάτω από το μειωμένο έτσι ώστε τα ίδια ψηφία να είναι το ένα κάτω από το άλλο και όλα τα κόμματα να βρίσκονται στην ίδια κάθετη στήλη. στα δεξιά, αποδίδουν, τουλάχιστον διανοητικά, στα μειωμένα ή αφαιρετικά τόσα μηδενικά ώστε να έχουν τον ίδιο αριθμό ψηφίων, μετά αφαιρούν με ψηφία, ξεκινώντας από τη δεξιά πλευρά, και στη διαφορά που προκύπτει βάζουν κόμμα στο ίδια κάθετη στήλη στην οποία βρίσκεται σε αναγωγή και αφαίρεση.
§ 109. Πολλαπλασιασμός δεκαδικών κλασμάτων.
Εξετάστε μερικά παραδείγματα πολλαπλασιασμού δεκαδικών κλασμάτων.
Για να βρούμε το γινόμενο αυτών των αριθμών, μπορούμε να συλλογιστούμε ως εξής: εάν ο παράγοντας αυξηθεί κατά 10 φορές, τότε και οι δύο παράγοντες θα είναι ακέραιοι και μπορούμε στη συνέχεια να τους πολλαπλασιάσουμε σύμφωνα με τους κανόνες για τον πολλαπλασιασμό των ακεραίων. Γνωρίζουμε όμως ότι όταν ένας από τους παράγοντες αυξάνεται πολλές φορές, το προϊόν αυξάνεται κατά το ίδιο ποσό. Αυτό σημαίνει ότι ο αριθμός που προκύπτει από τον πολλαπλασιασμό ακεραίων παραγόντων, δηλαδή 28 επί 23, είναι 10 φορές μεγαλύτερος από το πραγματικό γινόμενο και για να λάβετε το αληθινό γινόμενο, πρέπει να μειώσετε το προϊόν που βρέθηκε κατά 10 φορές. Επομένως, εδώ πρέπει να εκτελέσετε έναν πολλαπλασιασμό με το 10 μία φορά και μια διαίρεση με το 10 μία φορά, αλλά ο πολλαπλασιασμός και η διαίρεση με το 10 εκτελείται μετακινώντας το κόμμα δεξιά και αριστερά κατά ένα πρόσημο. Επομένως, πρέπει να το κάνετε αυτό: στον πολλαπλασιαστή, μετακινήστε το κόμμα προς τα δεξιά κατά ένα σύμβολο, από αυτό θα είναι ίσο με 23, τότε πρέπει να πολλαπλασιάσετε τους ακέραιους αριθμούς που προκύπτουν:
Αυτό το προϊόν είναι 10 φορές μεγαλύτερο από το πραγματικό. Επομένως, πρέπει να μειωθεί κατά 10 φορές, για το οποίο μετακινούμε το κόμμα με έναν χαρακτήρα προς τα αριστερά. Έτσι, παίρνουμε
28 2,3 = 64,4.
Για λόγους επαλήθευσης, μπορείτε να γράψετε ένα δεκαδικό κλάσμα με παρονομαστή και να εκτελέσετε μια ενέργεια σύμφωνα με τον κανόνα για τον πολλαπλασιασμό συνηθισμένων κλασμάτων, δηλ.
2) 12,27 0,021.
Η διαφορά μεταξύ αυτού του παραδείγματος και του προηγούμενου είναι ότι εδώ και οι δύο παράγοντες αντιπροσωπεύονται με δεκαδικά κλάσματα. Αλλά εδώ, στη διαδικασία του πολλαπλασιασμού, δεν θα δώσουμε προσοχή στα κόμματα, δηλαδή, θα αυξήσουμε προσωρινά τον πολλαπλασιαστή κατά 100 φορές και τον πολλαπλασιαστή κατά 1.000 φορές, πράγμα που θα αυξήσει το γινόμενο κατά 100.000 φορές. Έτσι, πολλαπλασιάζοντας το 1227 επί 21, παίρνουμε:
1 227 21 = 25 767.
Λαμβάνοντας υπόψη ότι το προϊόν που προκύπτει είναι 100.000 φορές μεγαλύτερο από το αληθινό, πρέπει τώρα να το μειώσουμε κατά 100.000 φορές τοποθετώντας σωστά ένα κόμμα σε αυτό, τότε παίρνουμε:
32,27 0,021 = 0,25767.
Ας ελέγξουμε:
Έτσι, για να πολλαπλασιάσουμε δύο δεκαδικά κλάσματα, αρκεί, χωρίς να δίνουμε προσοχή στα κόμματα, να τα πολλαπλασιάσουμε ως ακέραιους αριθμούς και στο γινόμενο να χωρίσουμε με κόμμα στη δεξιά πλευρά όσα δεκαδικά ψηφία υπήρχαν στον πολλαπλασιαστή και στο ο παράγοντας μαζί.
Στο τελευταίο παράδειγμα, το αποτέλεσμα είναι ένα γινόμενο με πέντε δεκαδικά ψηφία. Εάν δεν απαιτείται τέτοια μεγαλύτερη ακρίβεια, τότε γίνεται στρογγυλοποίηση του δεκαδικού κλάσματος. Κατά τη στρογγυλοποίηση, θα πρέπει να χρησιμοποιείτε τον ίδιο κανόνα που υποδεικνύεται για τους ακέραιους αριθμούς.
§ 110. Πολλαπλασιασμός με χρήση πινάκων.
Ο πολλαπλασιασμός των δεκαδικών αριθμών μπορεί μερικές φορές να γίνει χρησιμοποιώντας πίνακες. Για το σκοπό αυτό, μπορείτε, για παράδειγμα, να χρησιμοποιήσετε αυτούς τους πίνακες πολλαπλασιασμού των διψήφιων αριθμών, η περιγραφή των οποίων δόθηκε προηγουμένως.
1) Πολλαπλασιάστε το 53 επί 1,5.
Θα πολλαπλασιάσουμε το 53 επί 15. Στον πίνακα, αυτό το γινόμενο είναι ίσο με 795. Βρήκαμε το γινόμενο του 53 επί 15, αλλά ο δεύτερος παράγοντας μας ήταν 10 φορές μικρότερος, που σημαίνει ότι το γινόμενο πρέπει να μειωθεί κατά 10 φορές, δηλ.
53 1,5 = 79,5.
2) Πολλαπλασιάστε το 5,3 με το 4,7.
Αρχικά, ας βρούμε το γινόμενο του 53 επί 47 στον πίνακα, θα είναι 2491. Αλλά επειδή αυξήσαμε τον πολλαπλασιαστή και τον πολλαπλασιαστή κατά συνολικά 100 φορές, τότε το γινόμενο που προκύπτει είναι 100 φορές μεγαλύτερο από ό,τι θα έπρεπε. οπότε πρέπει να μειώσουμε αυτό το προϊόν κατά 100:
5,3 4,7 = 24,91.
3) Πολλαπλασιάστε το 0,53 επί 7,4.
Πρώτα βρίσκουμε στον πίνακα το γινόμενο 53 επί 74. Θα είναι 3.922. Αλλά επειδή έχουμε αυξήσει τον πολλαπλασιαστή κατά 100 φορές και τον πολλαπλασιαστή κατά 10 φορές, το γινόμενο έχει αυξηθεί κατά 1.000 φορές. οπότε τώρα πρέπει να το μειώσουμε κατά 1.000:
0,53 7,4 = 3,922.
§ 111. Διαίρεση δεκαδικών.
Θα δούμε τη δεκαδική διαίρεση με αυτή τη σειρά:
1. Διαίρεση δεκαδικού κλάσματος με ακέραιο,
1. Διαίρεση δεκαδικού κλάσματος με ακέραιο.
1) Διαιρέστε το 2,46 με το 2.
Διαιρέσαμε με 2 πρώτους ακέραιους, μετά δέκατα και τέλος εκατοστά.
2) Διαιρέστε το 32,46 με το 3.
32,46: 3 = 10,82.
Χωρίσαμε 3 δεκάδες με 3 και μετά αρχίσαμε να διαιρούμε 2 μονάδες με 3. Εφόσον ο αριθμός των μονάδων του μερίσματος (2) είναι μικρότερος από τον διαιρέτη (3), έπρεπε να βάλουμε 0 στο πηλίκο. Επιπλέον, στο υπόλοιπο γκρεμίσαμε 4 δέκατα και διαιρέσαμε τα 24 δέκατα με το 3. έλαβε ιδιωτικά 8 δέκατα και τελικά διαίρεσε 6 εκατοστά.
3) Διαιρέστε το 1,2345 με το 5.
1,2345: 5 = 0,2469.
Εδώ, στο πηλίκο αρχικά, βγήκαν μηδέν ακέραιοι, αφού ένας ακέραιος δεν διαιρείται με το 5.
4) Διαιρέστε το 13,58 με το 4.

Η ιδιαιτερότητα αυτού του παραδείγματος είναι ότι όταν πήραμε 9 εκατοστά ιδιωτικά, τότε βρέθηκε ένα υπόλοιπο ίσο με 2 εκατοστά, χωρίσαμε αυτό το υπόλοιπο σε χιλιοστά, πήραμε 20 χιλιοστά και φέραμε τη διαίρεση στο τέλος.
Κανόνας.Η διαίρεση ενός δεκαδικού κλάσματος με έναν ακέραιο πραγματοποιείται με τον ίδιο τρόπο όπως η διαίρεση των ακεραίων και τα υπόλοιπα που προκύπτουν μετατρέπονται σε δεκαδικά κλάσματα, όλο και πιο μικρά. Η διαίρεση συνεχίζεται μέχρι το υπόλοιπο να μηδενιστεί.
2. Διαίρεση δεκαδικού κλάσματος με δεκαδικό κλάσμα.
1) Διαιρέστε το 2,46 με το 0,2.
Γνωρίζουμε ήδη πώς να διαιρέσουμε ένα δεκαδικό κλάσμα με έναν ακέραιο. Ας σκεφτούμε μήπως και αυτή η νέα περίπτωση διαίρεσης μπορεί να αναχθεί στην προηγούμενη; Κάποτε, θεωρήσαμε την αξιοσημείωτη ιδιότητα του πηλίκου, η οποία συνίσταται στο γεγονός ότι παραμένει αμετάβλητο ενώ αυξάνει ή μειώνει το μέρισμα και τον διαιρέτη κατά τον ίδιο αριθμό φορές. Θα εκτελούσαμε εύκολα τη διαίρεση των αριθμών που μας προσφέρονται αν ο διαιρέτης ήταν ακέραιος. Για να γίνει αυτό, αρκεί να το αυξήσετε 10 φορές και για να λάβετε το σωστό πηλίκο, είναι απαραίτητο να αυξήσετε το μέρισμα κατά τον ίδιο αριθμό φορές, δηλαδή 10 φορές. Στη συνέχεια, η διαίρεση αυτών των αριθμών θα αντικατασταθεί από τη διαίρεση τέτοιων αριθμών:
και δεν χρειάζεται να γίνουν οποιεσδήποτε τροποποιήσεις ιδιωτικά.
Ας κάνουμε αυτή τη διαίρεση:
Άρα 2,46: 0,2 = 12,3.
2) Διαιρέστε το 1,25 με το 1,6.

Αυξάνουμε τον διαιρέτη (1,6) κατά 10 φορές. για να μην αλλάξει το πηλίκο, αυξάνουμε το μέρισμα κατά 10 φορές. 12 ακέραιοι δεν διαιρούνται με το 16, οπότε γράφουμε στο πηλίκο 0 και διαιρούμε τα 125 δέκατα με το 16, παίρνουμε 7 δέκατα στο πηλίκο και το υπόλοιπο είναι 13. Χωρίζουμε 13 δέκατα σε εκατοστά ορίζοντας μηδέν και διαιρούμε 130 εκατοστά με 16 κ.λπ. Δώστε προσοχή στα ακόλουθα:
α) όταν οι ακέραιοι αριθμοί δεν λαμβάνονται στο πηλίκο, τότε στη θέση τους γράφονται μηδενικοί ακέραιοι.
β) όταν, αφού ληφθεί το ψηφίο του μερίσματος στο υπόλοιπο, προκύπτει αριθμός που δεν διαιρείται με τον διαιρέτη, τότε γράφεται μηδέν στο πηλίκο.
γ) όταν, αφού αφαιρεθεί το τελευταίο ψηφίο του μερίσματος, η διαίρεση δεν τελειώνει, τότε, με την ανάθεση μηδενικών στα υπόλοιπα, η διαίρεση συνεχίζεται.
δ) εάν το μέρισμα είναι ακέραιος, τότε κατά τη διαίρεση του με δεκαδικό κλάσμα, η αύξησή του πραγματοποιείται με την ανάθεση μηδενικών σε αυτό.
Έτσι, για να διαιρέσετε έναν αριθμό με ένα δεκαδικό κλάσμα, πρέπει να απορρίψετε ένα κόμμα στον διαιρέτη και, στη συνέχεια, να αυξήσετε το μέρισμα όσες φορές αυξήθηκε ο διαιρέτης όταν έπεσε το κόμμα σε αυτό και στη συνέχεια να εκτελέσετε τη διαίρεση σύμφωνα με ο κανόνας της διαίρεσης του δεκαδικού κλάσματος με έναν ακέραιο.
§ 112. Πηλίκο κατά προσέγγιση.
Στην προηγούμενη παράγραφο, εξετάσαμε τη διαίρεση των δεκαδικών κλασμάτων και σε όλα τα παραδείγματα που λύσαμε, η διαίρεση έφτασε στο τέλος, δηλ. προέκυψε ένα ακριβές πηλίκο. Ωστόσο, στις περισσότερες περιπτώσεις το ακριβές πηλίκο δεν μπορεί να ληφθεί, όσο και αν επεκτείνουμε τη διαίρεση. Εδώ είναι μια τέτοια περίπτωση: Διαιρέστε το 53 με το 101.

Έχουμε ήδη λάβει πέντε ψηφία στο πηλίκο, αλλά η διαίρεση δεν έχει ακόμη τελειώσει και δεν υπάρχει καμία ελπίδα ότι θα τελειώσει ποτέ, αφού οι αριθμοί που έχουμε συναντήσει πριν αρχίζουν να εμφανίζονται στο υπόλοιπο. Οι αριθμοί θα επαναληφθούν επίσης στο πηλίκο: προφανώς, μετά τον αριθμό 7, θα εμφανιστεί ο αριθμός 5, μετά το 2 και ούτω καθεξής χωρίς τέλος. Σε τέτοιες περιπτώσεις, η διαίρεση διακόπτεται και περιορίζεται στα πρώτα λίγα ψηφία του πηλίκου. Αυτό το ιδιωτικό ονομάζεται κατά προσέγγιση.Πώς να εκτελέσετε τη διαίρεση σε αυτήν την περίπτωση, θα δείξουμε με παραδείγματα.
Έστω ότι απαιτείται η διαίρεση του 25 με το 3. Είναι προφανές ότι το ακριβές πηλίκο, που εκφράζεται ως ακέραιος ή δεκαδικό κλάσμα, δεν μπορεί να ληφθεί από μια τέτοια διαίρεση. Επομένως, θα αναζητήσουμε ένα κατά προσέγγιση πηλίκο:
25: 3 = 8 και υπόλοιπο 1
Το κατά προσέγγιση πηλίκο είναι 8. είναι, φυσικά, μικρότερο από το ακριβές πηλίκο, γιατί υπάρχει υπόλοιπο 1. Για να λάβετε το ακριβές πηλίκο, πρέπει να προσθέσετε στο κατά προσέγγιση πηλίκο που βρέθηκε, δηλαδή στο 8, το κλάσμα που προκύπτει από τη διαίρεση του υπολοίπου , ίσο με 1, επί 3; θα είναι κλάσμα 1/3. Αυτό σημαίνει ότι το ακριβές πηλίκο θα εκφραστεί ως μικτός αριθμός 8 1 / 3 . Αφού το 1/3 είναι σωστό κλάσμα, δηλαδή κλάσμα, λιγότερο από ένα, τότε, απορρίπτοντας το, υποθέτουμε λάθος, οι οποίες λιγότερο από ένα. Ιδιωτικός 8 θα κατά προσέγγιση πηλίκο μέχρι ένα με μειονέκτημα.Εάν πάρουμε το 9 αντί για το 8, τότε επιτρέπουμε επίσης ένα σφάλμα μικρότερο από ένα, αφού θα προσθέσουμε όχι ολόκληρη μονάδα, αλλά 2/3. Μια τέτοια ιδιωτική διαθήκη κατά προσέγγιση πηλίκο μέχρι ένα με περίσσεια.
Ας πάρουμε ένα άλλο παράδειγμα τώρα. Έστω ότι απαιτείται να διαιρεθεί το 27 με το 8. Επειδή εδώ δεν θα πάρουμε ένα ακριβές πηλίκο που εκφράζεται ως ακέραιος, θα αναζητήσουμε ένα κατά προσέγγιση πηλίκο:
27: 8 = 3 και υπόλοιπο 3.
Εδώ το σφάλμα είναι 3 / 8 , είναι μικρότερο από ένα, που σημαίνει ότι το κατά προσέγγιση πηλίκο (3) βρίσκεται μέχρι το ένα με ένα μειονέκτημα. Συνεχίζουμε τη διαίρεση: χωρίζουμε το υπόλοιπο των 3 σε δέκατα, παίρνουμε 30 δέκατα. Ας τα διαιρέσουμε με το 8.
Πήραμε ιδιωτικά επί τόπου δέκατα 3 και στα υπόλοιπα β δέκατα. Εάν περιοριστούμε συγκεκριμένα στον αριθμό 3.3 και απορρίψουμε το υπόλοιπο 6, τότε θα επιτρέψουμε ένα σφάλμα μικρότερο από το ένα δέκατο. Γιατί; Επειδή το ακριβές πηλίκο θα προέκυπτε όταν προσθέσαμε στο 3,3 το αποτέλεσμα της διαίρεσης των 6 δέκατων με το 8. από αυτή τη διαίρεση θα ήταν 6/80, που είναι λιγότερο από το ένα δέκατο. (Έλεγχος!) Έτσι, αν περιοριστούμε στα δέκατα στο πηλίκο, τότε μπορούμε να πούμε ότι βρήκαμε το πηλίκο ακρίβεια στο ένα δέκατο(με μειονέκτημα).
Ας συνεχίσουμε τη διαίρεση για να βρούμε ένα ακόμη δεκαδικό ψηφίο. Για να γίνει αυτό, χωρίζουμε 6 δέκατα σε εκατοστά και παίρνουμε 60 εκατοστά. Ας τα διαιρέσουμε με το 8.

Στο ιδιωτικό στην τρίτη θέση βγήκε 7 και στα υπόλοιπα 4 εκατοστά. αν τα απορρίψουμε, τότε επιτρέπουμε σφάλμα μικρότερο από το ένα εκατοστό, γιατί 4 εκατοστά διαιρούμενα με το 8 είναι μικρότερα από το εκατοστό. Σε τέτοιες περιπτώσεις, το πηλίκο λέγεται ότι βρίσκεται. ακρίβεια στο ένα εκατοστό(με μειονέκτημα).
Στο παράδειγμα που εξετάζουμε τώρα, μπορείτε να πάρετε το ακριβές πηλίκο, εκφρασμένο ως δεκαδικό κλάσμα. Για να γίνει αυτό, αρκεί να διαιρέσετε το τελευταίο υπόλοιπο, 4 εκατοστά, σε χιλιοστά και να διαιρέσετε με το 8.
Ωστόσο, στη συντριπτική πλειονότητα των περιπτώσεων, είναι αδύνατο να αποκτήσει κανείς ένα ακριβές πηλίκο και πρέπει να περιοριστεί στις κατά προσέγγιση τιμές του. Θα εξετάσουμε τώρα ένα τέτοιο παράδειγμα:
40: 7 = 5,71428571...
Οι τελείες στο τέλος του αριθμού δείχνουν ότι η διαίρεση δεν έχει ολοκληρωθεί, δηλαδή η ισότητα είναι κατά προσέγγιση. Συνήθως η κατά προσέγγιση ισότητα γράφεται ως εξής:
40: 7 = 5,71428571.
Πήραμε το πηλίκο με οκτώ δεκαδικά ψηφία. Αλλά αν δεν απαιτείται τέτοια μεγάλη ακρίβεια, μπορεί κανείς να περιοριστεί σε ολόκληρο το μέρος του πηλίκου, δηλαδή στον αριθμό 5 (ακριβέστερα, 6). Για μεγαλύτερη ακρίβεια, τα δέκατα θα μπορούσαν να ληφθούν υπόψη και το πηλίκο να ληφθεί ίσο με 5,7. αν για κάποιο λόγο αυτή η ακρίβεια είναι ανεπαρκής, τότε μπορούμε να σταματήσουμε στα εκατοστά και να πάρουμε 5,71 κ.λπ. Ας γράψουμε τα επιμέρους πηλίκα και ας τα ονομάσουμε.
Το πρώτο κατά προσέγγιση πηλίκο μέχρι το ένα 6.
Το δεύτερο » » » στο ένα δέκατο 5.7.
Τρίτο » » » έως ένα εκατοστό 5.71.
Τέταρτο » » » έως το ένα χιλιοστό του 5.714.
Έτσι, για να βρεθεί ένα κατά προσέγγιση πηλίκο μέχρι κάποιου, για παράδειγμα, του 3ου δεκαδικού ψηφίου (δηλαδή μέχρι το ένα χιλιοστό), η διαίρεση διακόπτεται μόλις βρεθεί αυτό το πρόσημο. Σε αυτή την περίπτωση, πρέπει να θυμόμαστε τον κανόνα που ορίζεται στην § 40.
§ 113. Τα πιο απλά προβλήματα για τόκο.
Αφού μελετήσουμε τα δεκαδικά κλάσματα, θα λύσουμε μερικά ακόμη ποσοστιαία προβλήματα.
Αυτά τα προβλήματα είναι παρόμοια με αυτά που λύσαμε στο τμήμα των συνηθισμένων κλασμάτων. αλλά τώρα θα γράψουμε τα εκατοστά με τη μορφή δεκαδικών κλασμάτων, δηλαδή χωρίς ρητά καθορισμένο παρονομαστή.
Πρώτα απ 'όλα, πρέπει να μπορείτε να μεταβείτε εύκολα από ένα συνηθισμένο κλάσμα σε ένα δεκαδικό κλάσμα με παρονομαστή 100. Για να το κάνετε αυτό, πρέπει να διαιρέσετε τον αριθμητή με τον παρονομαστή:

Ο παρακάτω πίνακας δείχνει πώς ένας αριθμός με σύμβολο % (ποσοστό) αντικαθίσταται από δεκαδικό με παρονομαστή 100:

Ας εξετάσουμε τώρα μερικά προβλήματα.
1. Εύρεση ποσοστών ενός δεδομένου αριθμού.
Εργασία 1.Μόνο 1.600 άνθρωποι ζουν σε ένα χωριό. Ο αριθμός των παιδιών σχολικής ηλικίας είναι 25% του συνολικού πληθυσμού. Πόσα παιδιά σχολικής ηλικίας είναι σε αυτό το χωριό;
Σε αυτό το πρόβλημα, πρέπει να βρείτε το 25%, ή το 0,25, του 1.600. Το πρόβλημα λύνεται πολλαπλασιάζοντας:
1.600 0,25 = 400 (παιδιά).
Επομένως, το 25% των 1.600 είναι 400.
Για μια σαφή κατανόηση αυτού του καθήκοντος, είναι χρήσιμο να υπενθυμίσουμε ότι για κάθε εκατό του πληθυσμού υπάρχουν 25 παιδιά σχολικής ηλικίας. Επομένως, για να βρείτε τον αριθμό όλων των παιδιών σχολικής ηλικίας, μπορείτε πρώτα να μάθετε πόσες εκατοντάδες υπάρχουν στον αριθμό 1600 (16) και στη συνέχεια να πολλαπλασιάσετε το 25 με τον αριθμό των εκατοντάδων (25 x 16 = 400). Με αυτόν τον τρόπο μπορείτε να ελέγξετε την εγκυρότητα της λύσης.
Εργασία 2.Τα ταμιευτήρια παρέχουν στους καταθέτες το 2% του εισοδήματος ετησίως. Πόσο εισόδημα ετησίως θα λάβει ένας καταθέτης που έχει καταθέσει: α) 200 ρούβλια; β) 500 ρούβλια; γ) 750 ρούβλια; δ) 1000 ρούβλια;
Και στις τέσσερις περιπτώσεις, για να λυθεί το πρόβλημα, θα χρειαστεί να υπολογίσετε το 0,02 από τα αναφερόμενα ποσά, δηλαδή, καθένας από αυτούς τους αριθμούς θα πρέπει να πολλαπλασιαστεί με 0,02. Ας το κάνουμε:
α) 200 0,02 = 4 (ρούβλια),
β) 500 0,02 = 10 (ρούβλια),
γ) 750 0,02 = 15 (ρούβλια),
δ) 1.000 0,02 = 20 (ρούβλια).
Κάθε μία από αυτές τις περιπτώσεις μπορεί να επαληθευτεί με τα ακόλουθα στοιχεία. Τα ταμιευτήρια δίνουν στους καταθέτες το 2% του εισοδήματος, δηλαδή το 0,02 του ποσού που τοποθετείται στις αποταμιεύσεις. Εάν το ποσό ήταν 100 ρούβλια, τότε το 0,02 από αυτό θα ήταν 2 ρούβλια. Αυτό σημαίνει ότι κάθε εκατό φέρνει στον καταθέτη 2 ρούβλια. εισόδημα. Επομένως, σε καθεμία από τις περιπτώσεις που εξετάζονται, αρκεί να υπολογίσετε πόσες εκατοντάδες είναι σε έναν δεδομένο αριθμό και να πολλαπλασιάσετε 2 ρούβλια με αυτόν τον αριθμό εκατοντάδων. Στο παράδειγμα α) εκατοντάδες 2, άρα
2 2 \u003d 4 (ρούβλια).
Στο παράδειγμα δ) οι εκατοντάδες είναι 10, που σημαίνει
2 10 \u003d 20 (ρούβλια).
2. Εύρεση αριθμού κατά το ποσοστό του.
Εργασία 1.Την άνοιξη, το σχολείο αποφοίτησε 54 μαθητές, που είναι το 6% του συνόλου των μαθητών. Πόσοι μαθητές ήταν στο σχολείο κατά το τελευταίο ακαδημαϊκό έτος;
Ας διευκρινίσουμε πρώτα το νόημα αυτού του προβλήματος. Στο σχολείο αποφοίτησαν 54 μαθητές, δηλαδή το 6% του συνόλου των μαθητών ή, με άλλα λόγια, τα 6 εκατοστά (0,06) του συνόλου των μαθητών του σχολείου. Αυτό σημαίνει ότι γνωρίζουμε το μέρος των μαθητών που εκφράζεται με τον αριθμό (54) και το κλάσμα (0,06), και από αυτό το κλάσμα πρέπει να βρούμε τον ακέραιο αριθμό. Έτσι, μπροστά μας είναι ένα συνηθισμένο πρόβλημα εύρεσης ενός αριθμού με το κλάσμα του (§ 90 σελ. 6). Προβλήματα αυτού του τύπου επιλύονται με διαίρεση:
Αυτό σημαίνει ότι στο σχολείο φοιτούσαν 900 μαθητές.
Είναι χρήσιμο να ελέγχετε τέτοια προβλήματα λύνοντας το αντίστροφο πρόβλημα, δηλαδή αφού λύσετε το πρόβλημα, θα πρέπει, τουλάχιστον στο μυαλό σας, να λύσετε το πρόβλημα του πρώτου τύπου (βρίσκοντας το ποσοστό ενός δεδομένου αριθμού): πάρτε τον αριθμό που βρέθηκε ( 900) όπως δίνεται και βρείτε το ποσοστό που υποδεικνύεται στο λυμένο πρόβλημα από αυτό, δηλαδή:
900 0,06 = 54.
Εργασία 2.Η οικογένεια ξοδεύει 780 ρούβλια για φαγητό κατά τη διάρκεια του μήνα, που είναι το 65% του μηνιαίου εισοδήματος του πατέρα. Προσδιορίστε το μηνιαίο εισόδημά του.
Αυτή η εργασία έχει την ίδια σημασία με την προηγούμενη. Δίνει μέρος των μηνιαίων κερδών, εκφρασμένα σε ρούβλια (780 ρούβλια) και υποδεικνύει ότι αυτό το μέρος είναι το 65%, ή το 0,65, των συνολικών κερδών. Και το επιθυμητό είναι όλα τα κέρδη:
780: 0,65 = 1 200.
Επομένως, τα επιθυμητά κέρδη είναι 1200 ρούβλια.
3. Εύρεση του ποσοστού των αριθμών.
Εργασία 1.Η σχολική βιβλιοθήκη διαθέτει συνολικά 6.000 βιβλία. Ανάμεσά τους είναι 1.200 βιβλία για τα μαθηματικά. Τι ποσοστό των βιβλίων μαθηματικών αποτελεί το συνολικό αριθμό των βιβλίων της βιβλιοθήκης;
Έχουμε ήδη εξετάσει (§97) αυτού του είδους το πρόβλημα και καταλήξαμε στο συμπέρασμα ότι για να υπολογίσετε το ποσοστό δύο αριθμών, πρέπει να βρείτε την αναλογία αυτών των αριθμών και να την πολλαπλασιάσετε με το 100.
Στην εργασία μας, πρέπει να βρούμε το ποσοστό των αριθμών 1.200 και 6.000.
Αρχικά βρίσκουμε την αναλογία τους και στη συνέχεια την πολλαπλασιάζουμε επί 100:
![]()
Έτσι, το ποσοστό των αριθμών 1.200 και 6.000 είναι 20. Με άλλα λόγια, τα βιβλία μαθηματικών αποτελούν το 20% του συνολικού αριθμού όλων των βιβλίων.
Για να ελέγξουμε, λύνουμε το αντίστροφο πρόβλημα: βρείτε το 20% των 6.000:
6 000 0,2 = 1 200.
Εργασία 2.Το εργοστάσιο θα πρέπει να λάβει 200 τόνους άνθρακα. Έχουν ήδη παραδοθεί 80 τόνοι Ποιο ποσοστό άνθρακα έχει παραδοθεί στο εργοστάσιο;
Αυτό το πρόβλημα ρωτά τι ποσοστό είναι ένας αριθμός (80) ενός άλλου (200). Η αναλογία αυτών των αριθμών θα είναι 80/200. Ας το πολλαπλασιάσουμε επί 100:
![]()
Αυτό σημαίνει ότι έχει παραδοθεί το 40% του άνθρακα.
Ορθογώνιο παραλληλόγραμμο?
Λύση. Από 2,88 dm2 \u003d 288 cm2 και 0,8 dm \u003d 8 cm, το μήκος του ορθογωνίου είναι 288: 8, δηλαδή 36 cm \u003d 3,6 dm. Βρήκαμε έναν αριθμό 3,6 τέτοιο ώστε 3,6 0,8 = 2,88. Είναι το πηλίκο του 2,88 διαιρούμενο με το 0,8.
Γράφουν: 2,88: 0,8 = 3,6.
Η απάντηση 3.6 μπορεί να ληφθεί χωρίς να μετατραπούν τα δεκατόμετρα σε εκατοστά. Για να το κάνετε αυτό, πολλαπλασιάστε τον διαιρέτη 0,8 και το μέρισμα 2,88 με 10 (δηλαδή, μετακινήστε το κόμμα ένα ψηφίο προς τα δεξιά σε αυτά) και διαιρέστε το 28,8 με 8. Και πάλι παίρνουμε: 28,8: 8 = 3,6.
Για να διαιρέσετε έναν αριθμό με ένα δεκαδικό κλάσμα, χρειάζεστε:
1) στο μέρισμα και στο διαιρέτη, μετακινήστε το κόμμα προς τα δεξιά κατά τόσα ψηφία όσα υπάρχουν μετά την υποδιαστολή στον διαιρέτη.
2) μετά από αυτό να γίνει διαίρεση με φυσικό αριθμό.
Παράδειγμα 1Διαιρέστε το 12.096 με το 2.24. Μετακινήστε τα κόμματα 2 ψηφία προς τα δεξιά στο μέρισμα και στο διαιρέτη. Παίρνουμε τους αριθμούς 1209,6 και 224. Από το 1209,6: 224 = 5,4, τότε 12,096: 2,24 = 5,4.
Παράδειγμα 2Διαιρέστε το 4,5 με το 0,125. Εδώ είναι απαραίτητο να μετακινήσετε το κόμμα 3 ψηφία προς τα δεξιά στο μέρισμα και το διαιρέτη. Δεδομένου ότι υπάρχει μόνο ένα ψηφίο μετά την υποδιαστολή στο μέρισμα, θα προσθέσουμε δύο μηδενικά σε αυτό στα δεξιά. Αφού μετακινήσουμε το κόμμα, παίρνουμε αριθμοί 4500 και 125. Από το 4500: 125 = 36, τότε 4,5: 0,125 = 36.
Από τα παραδείγματα 1 και 2, μπορεί να φανεί ότι όταν ένας αριθμός διαιρείται με ένα ακατάλληλο κλάσμα, αυτός ο αριθμός μειώνεται ή δεν αλλάζει και όταν διαιρείται με ένα σωστό δεκαδικό κλάσμα, αυξάνεται: 12.096\u003e 5.4 και 4.5< 36.
Διαιρέστε το 2,467 με το 0,01. Αφού μετακινήσουμε το κόμμα στο μέρισμα και τον διαιρέτη κατά 2 ψηφία προς τα δεξιά, παίρνουμε ότι το πηλίκο είναι 246,7: 1, δηλαδή 246,7.
Ως εκ τούτου, και 2,467: 0,01 = 246,7. Από εδώ παίρνουμε τον κανόνα:
Για να διαιρέσετε ένα δεκαδικό με 0,1. 0,01; 0,001, είναι απαραίτητο να μετακινήσετε το κόμμα σε αυτό προς τα δεξιά κατά τόσα ψηφία όσα μηδενικά υπάρχουν μπροστά από τη μονάδα στον διαιρέτη (δηλαδή, πολλαπλασιάστε το με 10, 100, 1000).
Εάν δεν υπάρχουν αρκετοί αριθμοί, πρέπει πρώτα να αποδώσετε στο τέλος κλάσματαμερικά μηδενικά.
Για παράδειγμα, 56,87: 0,0001 = 56,8700: 0,0001 = 568.700.
Διατυπώστε τον κανόνα για τη διαίρεση ενός δεκαδικού κλάσματος: με ένα δεκαδικό κλάσμα. κατά 0,1; 0,01; 0,001.
Ποιος αριθμός μπορεί να πολλαπλασιαστεί για να αντικαταστήσει τη διαίρεση με το 0,01;
1443. Βρείτε το πηλίκο και δοκιμάστε με πολλαπλασιασμό:
α) 0,8: 0,5; β) 3,51: 2,7; γ) 14.335: 0.61.
1444. Βρείτε το πηλίκο και δοκιμάστε με διαίρεση:
α) 0,096: 0,12; β) 0,126: 0,9; γ) 42.105: 3.5.
α) 7,56: 0,6; ζ) 6.944: 3.2; m) 14.976: 0.72;
β) 0,161: 0,7; η) 0,0456: 3,8; ιε) 168.392: 5.6;
γ) 0,468: 0,09; i) 0,182: 1,3; η) 24.576: 4.8;
δ) 0,00261: 0,03; ι) 131,67: 5,7; p) 16.51: 1.27;
ε) 0,824: 0,8; ια) 189,54: 0,78; γ) 46,08: 0,384;
ε) 10,5: 3,5; m) 636: 0,12; κ) 22.256: 20.8.
1446. Να γράψετε τις εκφράσεις:
α) 10 - 2,4x = 3,16; ε) 4,2p - p = 5,12;
β) (y + 26,1) 2,3 = 70,84; στ) 8,2t - 4,4t = 38,38;
γ) (z - 1,2): 0,6 = 21,1; ζ) (10,49 - s): 4,02 = 0,805;
δ) 3,5 m + m = 9,9; η) 9k - 8,67k = 0,6699.
1460. Σε δύο δεξαμενές υπήρχαν 119,88 τόνοι βενζίνης. Στο πρώτο ρεζερβουάρ είχε περισσότερη βενζίνη από ό,τι στο δεύτερο, κατά 1,7 φορές. Πόση βενζίνη υπήρχε σε κάθε ρεζερβουάρ;
1461. Από τρία αγροτεμάχια συγκομίστηκαν 87,36 τόνοι λάχανο. Ταυτόχρονα, συγκεντρώθηκαν 1,4 φορές περισσότερα από την πρώτη ενότητα και 1,8 φορές περισσότερα από τη δεύτερη ενότητα από ό,τι από την τρίτη ενότητα. Πόσοι τόνοι λάχανου συγκομίστηκαν από κάθε αγροτεμάχιο;
1462. Ένα καγκουρό είναι 2,4 φορές χαμηλότερο από μια καμηλοπάρδαλη, και μια καμηλοπάρδαλη είναι 2,52 μ. ψηλότερα από ένα καγκουρό Ποιο είναι το ύψος μιας καμηλοπάρδαλης και ποιο το ύψος ενός καγκουρό;
1463. Δύο πεζοί βρίσκονταν σε απόσταση 4,6 χλμ. μεταξύ τους. Πήγαν ο ένας προς τον άλλο και συναντήθηκαν σε 0,8 ώρες Βρείτε την ταχύτητα του κάθε πεζού αν η ταχύτητα του ενός είναι 1,3 φορές την ταχύτητα του άλλου.
1464. Κάντε τα εξής:
α) (130,2 - 30,8): 2,8 - 21,84:
β) 8.16: (1.32 + 3.48) - 0.345;
γ) 3,712: (7 - 3,8) + 1,3 (2,74 + 0,66);
δ) (3,4: 1,7 + 0,57: 1,9) 4,9 + 0,0825: 2,75;
ε) (4,44: 3,7 - 0,56: 2,8): 0,25 - 0,8;
στ) 10,79: 8,3 0,7 - 0,46 3,15: 6,9.
1465. Μετατρέψτε ένα κοινό κλάσμα σε δεκαδικό και βρείτε την τιμή εκφράσεις:

1466. Υπολογίστε προφορικά:
α) 25,5: 5; β) 9 0,2; γ) 0,3: 2; δ) 6,7 - 2,3;
1,5: 3; 1 0,1; 2:5; 6- 0,02;
4,7: 10; 16 0,01; 17,17: 17; 3,08 + 0,2;
0,48: 4; 24 0,3; 25,5: 25; 2,54 + 0,06;
0,9:100; 0,5 26; 0,8:16; 8,2-2,2.
1467. Βρείτε το έργο:
α) 0,1 0,1; δ) 0,4 0,4; ζ) 0,7 0,001;
β) 1,3 1,4; ε) 0,06 0,8; η) 100 0,09;
γ) 0,3 0,4; στ) 0,01 100; θ) 0,3 0,3 0,3.
1468. Βρείτε: 0,4 του αριθμού 30; 0,5 αριθμός 18; 0,1 αριθμοί 6,5; 2,5 αριθμοί 40; 0,12 αριθμός 100; 0,01 από 1000.
1469. Τι σημαίνει η έκφραση 5683.25a με a = 10; 0,1; 0,01; 100; 0,001; 1000; 0,00001;
1470. Σκεφτείτε ποιος από τους αριθμούς μπορεί να είναι ακριβής, οι οποίοι είναι κατά προσέγγιση:
α) υπάρχουν 32 μαθητές στην τάξη.
β) η απόσταση από τη Μόσχα στο Κίεβο είναι 900 km.
γ) το παραλληλεπίπεδο έχει 12 άκρες.
δ) μήκος τραπεζιού 1,3 m.
ε) ο πληθυσμός της Μόσχας είναι 8 εκατομμύρια άνθρωποι.
στ) 0,5 κιλό αλεύρι σε σακουλάκι.
ζ) η έκταση του νησιού της Κούβας είναι 105.000 km2.
η) υπάρχουν 10.000 βιβλία στη σχολική βιβλιοθήκη.
i) ένα άνοιγμα είναι ίσο με 4 vershok, και ένα vershok είναι ίσο με 4,45 cm (vershok
το μήκος της φάλαγγας του δείκτη).
1471. Βρείτε τρεις λύσεις για την ανίσωση:
α) 1.2< х < 1,6; в) 0,001 < х < 0,002;
β) 2.1< х< 2,3; г) 0,01 <х< 0,011.
1472. Συγκρίνετε, χωρίς να υπολογίσετε, τις τιμές των παραστάσεων:
α) 24 0,15 και (24 - 15): 100;
β) 0,084 0,5 και (84 5): 10.000.
Εξήγησε την απάντησή σου.
1473. Στρογγυλοποιήστε τους αριθμούς:

1474. Εκτελέστε διαίρεση:
α) 22,7: 10; 23.3:10; 3.14:10; 9.6:10;
β) 304: 100; 42,5:100; 2.5:100; 0,9:100; 0,03:100;
γ) 143,4: 12; 1.488:124; 0,3417: 34; 159.9:235; 65.32:568.
1475. Ένας ποδηλάτης έφυγε από το χωριό με ταχύτητα 12 χλμ./ώρα. Μετά από 2 ώρες, ένας άλλος ποδηλάτης έφυγε από το ίδιο χωριό προς την αντίθετη κατεύθυνση,
και η ταχύτητα του δεύτερου είναι 1,25 φορές η ταχύτητα του πρώτου. Ποια είναι η απόσταση μεταξύ τους 3,3 ώρες μετά την αναχώρηση του δεύτερου ποδηλάτη;
1476. Η ταχύτητα του σκάφους είναι 8,5 km/h και η ταχύτητα του ρεύματος είναι 1,3 km/h. Πόσο μακριά θα ταξιδέψει το σκάφος με το ρεύμα σε 3,5 ώρες; Πόσο μακριά θα ταξιδέψει το σκάφος ανάντη σε 5,6 ώρες;
1477. Το εργοστάσιο κατασκεύασε 3,75 χιλιάδες εξαρτήματα και τα πούλησε στην τιμή των 950 ρούβλια. ένα κομμάτι. Το κόστος του εργοστασίου για την κατασκευή ενός μέρους ανήλθε σε 637,5 ρούβλια. Βρείτε το κέρδος που αποκόμισε το εργοστάσιο από την πώληση αυτών των ανταλλακτικών.
1478. Το πλάτος ενός ορθογώνιου παραλληλεπιπέδου είναι 7,2 cm, το οποίο είναι ![]() Βρείτε τον όγκο αυτού του πλαισίου και στρογγυλοποιήστε την απάντησή σας στον πλησιέστερο ακέραιο.
Βρείτε τον όγκο αυτού του πλαισίου και στρογγυλοποιήστε την απάντησή σας στον πλησιέστερο ακέραιο.
1479. Ο Πάπας Κάρλο υποσχέθηκε να δίνει στον Πιέρο 4 σολίντι κάθε μέρα και στον Πινόκιο 1 σολίντι την πρώτη μέρα και 1 στρατιώτη περισσότερο κάθε επόμενη μέρα, αν συμπεριφερόταν καλά. Ο Πινόκιο προσβλήθηκε: αποφάσισε ότι, όσο σκληρά κι αν προσπάθησε, δεν θα κατάφερνε ποτέ να πάρει τόσο πολύ σόιντ συνολικά όσο ο Πιερό. Σκεφτείτε αν ο Πινόκιο έχει δίκιο.
1480. 231 μέτρα σανίδων πήγαν σε 3 ντουλάπια και 9 ράφια, και 4 φορές περισσότερο υλικό πηγαίνει στο ντουλάπι παρά στο ράφι. Πόσα μέτρα σανίδες πηγαίνουν στο ντουλάπι και πόσα - στο ράφι;
1481. Λύστε το πρόβλημα:
1) Ο πρώτος αριθμός είναι 6,3 και είναι ο δεύτερος αριθμός. Ο τρίτος αριθμός είναι ο δεύτερος. Βρείτε τον δεύτερο και τον τρίτο αριθμό.
2) Ο πρώτος αριθμός είναι 8.1. Ο δεύτερος αριθμός είναι από τον πρώτο αριθμό και από τον τρίτο αριθμό. Βρείτε τον δεύτερο και τον τρίτο αριθμό.
1482. Βρείτε την τιμή της παράστασης:
1) (7 - 5,38) 2,5;
2) (8 - 6,46) 1,5.
1483. Βρείτε την τιμή του ιδιωτικού:
α) 17.01: 6.3; δ) 1,4245: 3,5; ζ) 0,02976: 0,024;
β) 1.598: 4.7; ε) 193,2: 8,4; η) 11,59: 3,05;
γ) 39.156: 7.8; ε) 0,045: 0,18; θ) 74.256: 18.2.
1484. Το μονοπάτι από το σπίτι στο σχολείο είναι 1,1 χλμ. Το κορίτσι διανύει αυτό το μονοπάτι σε 0,25 ώρες Πόσο γρήγορα περπατάει το κορίτσι;
1485. Σε ένα διαμέρισμα δύο δωματίων, η επιφάνεια ενός δωματίου είναι 20,64 m 2 και η επιφάνεια του άλλου δωματίου είναι 2,4 φορές μικρότερη. Βρείτε την περιοχή αυτών των δύο δωματίων μαζί.
1486. Ο κινητήρας καταναλώνει 111 λίτρα καυσίμου σε 7,5 ώρες. Πόσα λίτρα καυσίμου θα καταναλώσει ο κινητήρας σε 1,8 ώρες;
1487. Ένα μεταλλικό μέρος με όγκο 3,5 dm3 έχει μάζα 27,3 kg. Ένα άλλο αντικείμενο από το ίδιο μέταλλο έχει μάζα 10,92 kg. Ποιος είναι ο όγκος του δεύτερου μέρους;
1488. 2,28 τόνοι βενζίνης χύθηκαν στη δεξαμενή μέσω δύο σωλήνων. 3,6 τόνοι βενζίνης την ώρα περνούσαν από τον πρώτο σωλήνα και ήταν ανοιχτός για 0,4 ώρες, 0,8 τόνοι βενζίνη λιγότεροι από τον πρώτο σωλήνα έμπαιναν ανά ώρα από τον δεύτερο σωλήνα. Πόσο καιρό ήταν ανοιχτός ο δεύτερος σωλήνας;
1489. Λύστε την εξίσωση:
α) 2,136: (1,9 - x) = 7,12; γ) 0,2t + 1,7t - 0,54 = 0,22;
β) 4,2 (0,8 + y) = 8,82; δ) 5,6 g - 2z - 0,7z + 2,65 = 7.
1490. Εμπορεύματα βάρους 13,3 τόνων μοιράστηκαν σε τρία οχήματα. Το πρώτο αυτοκίνητο φορτώθηκε 1,3 φορές περισσότερο και το δεύτερο - 1,5 φορές περισσότερο από το τρίτο αυτοκίνητο. Πόσοι τόνοι εμπορευμάτων φορτώθηκαν σε κάθε όχημα;
1491. Δύο πεζοί έφυγαν ταυτόχρονα από το ίδιο σημείο προς αντίθετες κατευθύνσεις. Μετά από 0,8 ώρες, η απόσταση μεταξύ τους έγινε ίση με 6,8 χιλιόμετρα. Η ταχύτητα του ενός πεζού ήταν 1,5 φορές μεγαλύτερη από την ταχύτητα του άλλου. Βρείτε την ταχύτητα του κάθε πεζού.
1492. Κάντε τα εξής:
α) (21,2544: 0,9 + 1,02 3,2): 5,6;
β) 4,36: (3,15 + 2,3) + (0,792 - 0,78) 350;
γ) (3,91: 2,3 5,4 - 4,03) 2,4;
δ) 6,93: (0,028 + 0,36 4,2) - 3,5.
1493. Ένας γιατρός ήρθε στο σχολείο και έφερε 0,25 κιλά ορό για εμβολιασμό. Πόσα παιδιά μπορεί να κάνει ενέσεις εάν κάθε ένεση απαιτεί 0,002 κιλά ορού;
1494. Έφεραν στο κατάστημα 2,8 τόνοι μελόψωμο. Πριν από το μεσημεριανό γεύμα, αυτά τα μπισκότα με μελόψωμο πουλήθηκαν. Πόσοι τόνοι μελόψωμο απομένουν να πουληθούν;
1495. Από ένα κομμάτι ύφασμα κόπηκαν 5,6 μ. Πόσα μέτρα υφάσματος ήταν στο τεμάχιο αν κόπηκε αυτό το κομμάτι;
N.Ya. VILENKIN, V. I. ZHOKHOV, A. S. CHESNOKOV, S. I. SHVARTSBURD, Mathematics Grade 5, Textbook for Educational Institution
Στο σχολείο, αυτές οι ενέργειες μελετώνται από απλές έως σύνθετες. Επομένως, είναι σίγουρα απαραίτητο να κυριαρχήσετε τον αλγόριθμο για την εκτέλεση των παραπάνω πράξεων χρησιμοποιώντας απλά παραδείγματα. Έτσι ώστε αργότερα δεν θα υπάρχουν δυσκολίες με τη διαίρεση των δεκαδικών κλασμάτων σε μια στήλη. Μετά από όλα, αυτή είναι η πιο δύσκολη έκδοση τέτοιων εργασιών.
Αυτό το θέμα απαιτεί συνεπή μελέτη. Τα κενά στη γνώση είναι απαράδεκτα εδώ. Αυτή την αρχή πρέπει να μάθει κάθε μαθητής ήδη στην πρώτη τάξη. Επομένως, εάν παραλείψετε πολλά μαθήματα στη σειρά, θα πρέπει να κυριαρχήσετε μόνοι σας στο υλικό. Διαφορετικά, αργότερα θα υπάρξουν προβλήματα όχι μόνο με τα μαθηματικά, αλλά και με άλλα θέματα που σχετίζονται με αυτά.
Η δεύτερη προϋπόθεση για μια επιτυχημένη μελέτη των μαθηματικών είναι να προχωρήσουμε σε παραδείγματα διαίρεσης σε μια στήλη μόνο αφού έχουν κατακτηθεί η πρόσθεση, η αφαίρεση και ο πολλαπλασιασμός.
Θα είναι δύσκολο για ένα παιδί να διαιρέσει αν δεν έχει μάθει τον πίνακα πολλαπλασιασμού. Παρεμπιπτόντως, είναι καλύτερο να το μάθετε από τον Πυθαγόρειο πίνακα. Δεν υπάρχει τίποτα περιττό και ο πολλαπλασιασμός είναι πιο εύκολος στην πέψη σε αυτή την περίπτωση.
Πώς πολλαπλασιάζονται οι φυσικοί αριθμοί σε μια στήλη;
Εάν υπάρχει δυσκολία στην επίλυση παραδειγμάτων σε μια στήλη για διαίρεση και πολλαπλασιασμό, τότε είναι απαραίτητο να ξεκινήσετε την επίλυση του προβλήματος με πολλαπλασιασμό. Επειδή η διαίρεση είναι το αντίστροφο του πολλαπλασιασμού:
- Πριν πολλαπλασιάσετε δύο αριθμούς, πρέπει να τους εξετάσετε προσεκτικά. Επιλέξτε αυτό με περισσότερα ψηφία (μακρύτερα), γράψτε το πρώτα. Τοποθετήστε το δεύτερο κάτω από αυτό. Επιπλέον, οι αριθμοί της αντίστοιχης κατηγορίας θα πρέπει να βρίσκονται στην ίδια κατηγορία. Δηλαδή, το δεξιότερο ψηφίο του πρώτου αριθμού πρέπει να είναι πάνω από το δεξιότερο ψηφίο του δεύτερου.
- Πολλαπλασιάστε το δεξιότερο ψηφίο του κάτω αριθμού με κάθε ψηφίο του επάνω αριθμού, ξεκινώντας από τα δεξιά. Γράψε την απάντηση κάτω από τη γραμμή έτσι ώστε το τελευταίο της ψηφίο να βρίσκεται κάτω από αυτό με το οποίο πολλαπλασιάστηκε.
- Επαναλάβετε το ίδιο με το άλλο ψηφίο του κάτω αριθμού. Αλλά το αποτέλεσμα του πολλαπλασιασμού πρέπει να μετατοπιστεί ένα ψηφίο προς τα αριστερά. Σε αυτήν την περίπτωση, το τελευταίο ψηφίο του θα είναι κάτω από αυτό με το οποίο πολλαπλασιάστηκε.
Συνεχίστε αυτόν τον πολλαπλασιασμό σε μια στήλη μέχρι να εξαντληθούν οι αριθμοί του δεύτερου πολλαπλασιαστή. Τώρα πρέπει να διπλωθούν. Αυτή θα είναι η επιθυμητή απάντηση.

Αλγόριθμος για τον πολλαπλασιασμό σε μια στήλη δεκαδικών κλασμάτων
Πρώτον, υποτίθεται ότι δεν δίνονται δεκαδικά κλάσματα, αλλά φυσικά. Δηλαδή, αφαιρέστε κόμματα από αυτά και στη συνέχεια προχωρήστε όπως περιγράφεται στην προηγούμενη περίπτωση.
Η διαφορά αρχίζει όταν γράφεται η απάντηση. Σε αυτό το σημείο, είναι απαραίτητο να μετρηθούν όλοι οι αριθμοί που βρίσκονται μετά την υποδιαστολή και στα δύο κλάσματα. Αυτό είναι πόσα από αυτά πρέπει να μετρήσετε από το τέλος της απάντησης και να βάλετε κόμμα εκεί.
Είναι βολικό να επεξηγηθεί αυτός ο αλγόριθμος με ένα παράδειγμα: 0,25 x 0,33:

Πώς να αρχίσετε να μαθαίνετε να διαιρείτε;
Πριν λύσουμε παραδείγματα για διαίρεση σε στήλη, υποτίθεται ότι θυμόμαστε τα ονόματα των αριθμών που βρίσκονται στο παράδειγμα για διαίρεση. Το πρώτο από αυτά (αυτό που διαιρεί) είναι το διαιρετό. Το δεύτερο (διαιρούμενο με αυτό) είναι διαιρέτης. Η απάντηση είναι ιδιωτική.
Μετά από αυτό, χρησιμοποιώντας ένα απλό καθημερινό παράδειγμα, θα εξηγήσουμε την ουσία αυτής της μαθηματικής πράξης. Για παράδειγμα, αν πάρετε 10 γλυκά, τότε είναι εύκολο να τα μοιράσετε εξίσου μεταξύ της μαμάς και του μπαμπά. Τι γίνεται όμως αν χρειαστεί να τα μοιράσετε στους γονείς και τον αδερφό σας;
Μετά από αυτό, μπορείτε να εξοικειωθείτε με τους κανόνες της διαίρεσης και να τους κυριαρχήσετε με συγκεκριμένα παραδείγματα. Απλές στην αρχή και μετά προχωράμε σε όλο και πιο σύνθετες.
Αλγόριθμος για τη διαίρεση αριθμών σε στήλη

Αρχικά, παρουσιάζουμε τη διαδικασία για φυσικούς αριθμούς που διαιρούνται με μονοψήφιο αριθμό. Θα αποτελέσουν επίσης τη βάση για πολυψήφιους διαιρέτες ή δεκαδικά κλάσματα. Μόνο τότε υποτίθεται ότι θα γίνουν μικρές αλλαγές, αλλά περισσότερα για αυτό αργότερα:
- Πριν κάνετε τη διαίρεση σε μια στήλη, πρέπει να μάθετε πού είναι το μέρισμα και ο διαιρέτης.
- Καταγράψτε το μέρισμα. Στα δεξιά του υπάρχει ένα διαχωριστικό.
- Σχεδιάστε μια γωνία στα αριστερά και κάτω κοντά στην τελευταία γωνία.
- Προσδιορίστε το ημιτελές μέρισμα, δηλαδή τον αριθμό που θα είναι το ελάχιστο για διαίρεση. Συνήθως αποτελείται από ένα ψηφίο, το πολύ δύο.
- Επιλέξτε τον αριθμό που θα γραφεί πρώτος στην απάντηση. Πρέπει να είναι ο αριθμός των φορών που χωράει ο διαιρέτης στο μέρισμα.
- Γράψτε το αποτέλεσμα του πολλαπλασιασμού αυτού του αριθμού με έναν διαιρέτη.
- Γράψτε το κάτω από έναν ημιτελή διαιρέτη. Εκτελέστε αφαίρεση.
- Μεταφέρετε στο υπόλοιπο το πρώτο ψηφίο μετά το μέρος που έχει ήδη διαιρεθεί.
- Πάρτε ξανά την απάντηση.
- Επαναλάβετε τον πολλαπλασιασμό και την αφαίρεση. Εάν το υπόλοιπο είναι μηδέν και το μέρισμα έχει τελειώσει, τότε το παράδειγμα έχει ολοκληρωθεί. Διαφορετικά, επαναλάβετε τα βήματα: γκρεμίστε τον αριθμό, σηκώστε τον αριθμό, πολλαπλασιάστε, αφαιρέστε.
Πώς να λύσετε τη διαίρεση μεγάλου μήκους εάν υπάρχουν περισσότερα από ένα ψηφία στον διαιρέτη;
Ο ίδιος ο αλγόριθμος συμπίπτει πλήρως με αυτό που περιγράφηκε παραπάνω. Η διαφορά θα είναι ο αριθμός των ψηφίων στο ημιτελές μέρισμα. Τώρα θα πρέπει να υπάρχουν τουλάχιστον δύο από αυτά, αλλά αν αποδειχθούν λιγότερα από τον διαιρέτη, τότε υποτίθεται ότι λειτουργεί με τα τρία πρώτα ψηφία.
Υπάρχει μια άλλη απόχρωση σε αυτή τη διαίρεση. Το γεγονός είναι ότι το υπόλοιπο και ο αριθμός που μεταφέρεται σε αυτό μερικές φορές δεν διαιρούνται με διαιρέτη. Στη συνέχεια, υποτίθεται ότι αποδίδει ένα ακόμη σχήμα με τη σειρά. Αλλά ταυτόχρονα, η απάντηση πρέπει να είναι μηδενική. Εάν οι τριψήφιοι αριθμοί χωριστούν σε μια στήλη, τότε ίσως χρειαστεί να καταργηθούν περισσότερα από δύο ψηφία. Στη συνέχεια εισάγεται ο κανόνας: τα μηδενικά στην απάντηση πρέπει να είναι ένα λιγότερα από τον αριθμό των ψηφίων που αφαιρούνται.
Μπορείτε να εξετάσετε μια τέτοια διαίρεση χρησιμοποιώντας το παράδειγμα - 12082: 863.
- Το ημιτελές διαιρετό σε αυτό είναι ο αριθμός 1208. Ο αριθμός 863 τοποθετείται σε αυτό μόνο μία φορά. Επομένως, ως απάντηση, υποτίθεται ότι θα βάλει 1 και θα γράψει 863 κάτω από το 1208.
- Μετά την αφαίρεση, το υπόλοιπο είναι 345.
- Σε αυτόν πρέπει να κατεδαφίσετε τον αριθμό 2.
- Στον αριθμό 3452, το 863 χωράει τέσσερις φορές.
- Τέσσερα πρέπει να γραφτούν ως απάντηση. Επιπλέον, όταν πολλαπλασιαστεί με το 4, προκύπτει αυτός ο αριθμός.
- Το υπόλοιπο μετά την αφαίρεση είναι μηδέν. Δηλαδή ολοκληρώνεται η διαίρεση.
Η απάντηση στο παράδειγμα είναι 14.
Τι γίνεται αν το μέρισμα τελειώνει στο μηδέν;
Ή μερικά μηδενικά; Σε αυτήν την περίπτωση, προκύπτει ένα μηδενικό υπόλοιπο και εξακολουθούν να υπάρχουν μηδενικά στο μέρισμα. Μην απελπίζεστε, όλα είναι πιο εύκολα από ό,τι φαίνεται. Αρκεί απλώς να αποδώσουμε στην απάντηση όλα τα μηδενικά που έμειναν αδιαίρετα.
Για παράδειγμα, πρέπει να διαιρέσετε το 400 με το 5. Το ημιτελές μέρισμα είναι 40. Το πέντε τοποθετείται σε αυτό 8 φορές. Αυτό σημαίνει ότι η απάντηση υποτίθεται ότι γράφεται 8. Κατά την αφαίρεση, δεν υπάρχει υπόλοιπο. Δηλαδή, η διαίρεση τελείωσε, αλλά το μηδέν παραμένει στο μέρισμα. Θα πρέπει να προστεθεί στην απάντηση. Έτσι, διαιρώντας το 400 με το 5 δίνεται το 80.

Τι γίνεται αν χρειαστεί να διαιρέσετε ένα δεκαδικό;
Και πάλι, αυτός ο αριθμός μοιάζει με φυσικός αριθμός, αν όχι για το κόμμα που χωρίζει το ακέραιο από το κλασματικό μέρος. Αυτό υποδηλώνει ότι η διαίρεση των δεκαδικών κλασμάτων σε μια στήλη είναι παρόμοια με αυτή που περιγράφηκε παραπάνω.
Η μόνη διαφορά θα είναι το ερωτηματικό. Υποτίθεται ότι θα απαντηθεί αμέσως, μόλις αφαιρεθεί το πρώτο ψηφίο από το κλασματικό μέρος. Με άλλο τρόπο, μπορεί να ειπωθεί ως εξής: η διαίρεση του ακέραιου μέρους έχει τελειώσει - βάλτε κόμμα και συνεχίστε τη λύση περαιτέρω.
Όταν λύνετε παραδείγματα για διαίρεση σε στήλη με δεκαδικά κλάσματα, πρέπει να θυμάστε ότι οποιοσδήποτε αριθμός μηδενικών μπορεί να εκχωρηθεί στο τμήμα μετά την υποδιαστολή. Μερικές φορές αυτό είναι απαραίτητο για να συμπληρώσετε τους αριθμούς μέχρι το τέλος.

Διαίρεση δύο δεκαδικών
Μπορεί να φαίνεται περίπλοκο. Αλλά μόνο στην αρχή. Εξάλλου, ο τρόπος διαίρεσης σε μια στήλη κλασμάτων με έναν φυσικό αριθμό είναι ήδη ξεκάθαρος. Επομένως, πρέπει να αναγάγουμε αυτό το παράδειγμα στην ήδη γνωστή μορφή.
Καν'το εύκολο. Πρέπει να πολλαπλασιάσετε και τα δύο κλάσματα με 10, 100, 1.000 ή 10.000 ή ίσως ένα εκατομμύριο εάν το απαιτεί η εργασία. Ο πολλαπλασιαστής υποτίθεται ότι επιλέγεται με βάση πόσα μηδενικά υπάρχουν στο δεκαδικό μέρος του διαιρέτη. Δηλαδή, ως αποτέλεσμα, αποδεικνύεται ότι θα πρέπει να διαιρέσετε ένα κλάσμα με έναν φυσικό αριθμό.
Και θα είναι στη χειρότερη περίπτωση. Μετά από όλα, μπορεί να αποδειχθεί ότι το μέρισμα από αυτή τη λειτουργία γίνεται ακέραιος. Στη συνέχεια, η λύση του παραδείγματος με διαίρεση σε στήλη κλασμάτων θα μειωθεί στην απλούστερη επιλογή: πράξεις με φυσικούς αριθμούς.
Για παράδειγμα: 28,4 διαιρούμενο με 3,2:
- Πρώτον, πρέπει να πολλαπλασιαστούν με το 10, αφού στον δεύτερο αριθμό υπάρχει μόνο ένα ψηφίο μετά την υποδιαστολή. Ο πολλαπλασιασμός θα δώσει 284 και 32.
- Υποτίθεται ότι είναι χωρισμένοι. Και αμέσως ο ακέραιος αριθμός είναι 284 επί 32.
- Ο πρώτος αντιστοιχισμένος αριθμός για την απάντηση είναι 8. Πολλαπλασιάζοντας τον δίνουμε 256. Το υπόλοιπο είναι 28.
- Η διαίρεση του ακέραιου τμήματος έχει τελειώσει και υποτίθεται ότι μπαίνει κόμμα στην απάντηση.
- Κατεδάφιση στο υπόλοιπο 0.
- Πάρε πάλι 8.
- Υπόλοιπο: 24. Προσθέστε άλλο 0 σε αυτό.
- Τώρα πρέπει να πάρετε το 7.
- Το αποτέλεσμα του πολλαπλασιασμού είναι 224, το υπόλοιπο είναι 16.
- Κατεδάφισε άλλο 0. Πάρε 5 και πάρε ακριβώς 160. Το υπόλοιπο είναι 0.
Η διαίρεση ολοκληρώθηκε. Το αποτέλεσμα του παραδείγματος 28,4:3,2 είναι 8,875.
Τι γίνεται αν ο διαιρέτης είναι 10, 100, 0,1 ή 0,01;

Όπως και με τον πολλαπλασιασμό, έτσι και εδώ δεν χρειάζεται διαίρεση. Αρκεί απλώς να μετακινήσετε το κόμμα προς τη σωστή κατεύθυνση για έναν ορισμένο αριθμό ψηφίων. Επιπλέον, σύμφωνα με αυτήν την αρχή, μπορείτε να λύσετε παραδείγματα τόσο με ακέραιους όσο και με δεκαδικά κλάσματα.
Έτσι, εάν πρέπει να διαιρέσετε με το 10, το 100 ή το 1000, τότε το κόμμα μετακινείται προς τα αριστερά κατά τόσα ψηφία όσα μηδενικά υπάρχουν στον διαιρέτη. Δηλαδή, όταν ένας αριθμός διαιρείται με το 100, το κόμμα πρέπει να μετακινείται προς τα αριστερά κατά δύο ψηφία. Εάν το μέρισμα είναι φυσικός αριθμός, τότε θεωρείται ότι το κόμμα βρίσκεται στο τέλος του.
Αυτή η ενέργεια παράγει το ίδιο αποτέλεσμα σαν να πολλαπλασιαζόταν ο αριθμός με 0,1, 0,01 ή 0,001. Σε αυτά τα παραδείγματα, το κόμμα μετακινείται επίσης προς τα αριστερά με έναν αριθμό ψηφίων ίσο με το μήκος του κλασματικού μέρους.
Κατά τη διαίρεση με το 0,1 (κ.λπ.) ή τον πολλαπλασιασμό με το 10 (κ.λπ.), το κόμμα πρέπει να μετακινείται προς τα δεξιά κατά ένα ψηφίο (ή δύο, τρία, ανάλογα με τον αριθμό των μηδενικών ή το μήκος του κλασματικού μέρους).
Αξίζει να σημειωθεί ότι ο αριθμός των ψηφίων που δίνονται στο μέρισμα ενδέχεται να μην είναι επαρκής. Στη συνέχεια, τα μηδενικά που λείπουν μπορούν να αντιστοιχιστούν στα αριστερά (στο ακέραιο μέρος) ή στα δεξιά (μετά την υποδιαστολή).

Διαίρεση περιοδικών κλασμάτων
Σε αυτήν την περίπτωση, δεν θα μπορείτε να λάβετε την ακριβή απάντηση κατά τη διαίρεση σε στήλη. Πώς να λύσετε ένα παράδειγμα εάν συναντήσετε ένα κλάσμα με τελεία; Εδώ είναι απαραίτητο να προχωρήσουμε σε συνηθισμένα κλάσματα. Και στη συνέχεια εκτελέστε τη διαίρεση τους σύμφωνα με τους κανόνες που μελετήθηκαν προηγουμένως.
Για παράδειγμα, πρέπει να διαιρέσετε το 0, (3) με το 0,6. Το πρώτο κλάσμα είναι περιοδικό. Μετατρέπεται στο κλάσμα 3/9, το οποίο μετά την αναγωγή θα δώσει το 1/3. Το δεύτερο κλάσμα είναι το τελικό δεκαδικό. Είναι ακόμα πιο εύκολο να γράψετε ένα συνηθισμένο: 6/10, που ισούται με 3/5. Ο κανόνας για τη διαίρεση των συνηθισμένων κλασμάτων ορίζει την αντικατάσταση της διαίρεσης με πολλαπλασιασμό και του διαιρέτη με το αντίστροφο ενός αριθμού. Δηλαδή, το παράδειγμα καταλήγει στον πολλαπλασιασμό του 1/3 επί 5/3. Η απάντηση είναι 5/9.
Αν το παράδειγμα έχει διαφορετικά κλάσματα...
Στη συνέχεια, υπάρχουν πολλές πιθανές λύσεις. Αρχικά, μπορείτε να δοκιμάσετε να μετατρέψετε ένα συνηθισμένο κλάσμα σε δεκαδικό. Στη συνέχεια, διαιρέστε ήδη δύο δεκαδικά ψηφία σύμφωνα με τον παραπάνω αλγόριθμο.
Δεύτερον, κάθε τελικό δεκαδικό κλάσμα μπορεί να γραφτεί ως κοινό κλάσμα. Απλώς δεν είναι πάντα βολικό. Τις περισσότερες φορές, τέτοια κλάσματα αποδεικνύονται τεράστια. Ναι, και οι απαντήσεις είναι δυσκίνητες. Επομένως, η πρώτη προσέγγιση θεωρείται προτιμότερη.
Σε αυτό το άρθρο, θα αναλύσουμε μια τόσο σημαντική ενέργεια με δεκαδικά κλάσματα όπως η διαίρεση. Αρχικά, διατυπώνουμε τις γενικές αρχές και, στη συνέχεια, θα αναλύσουμε πώς να διαιρέσουμε σωστά τα δεκαδικά κλάσματα από μια στήλη τόσο σε άλλα κλάσματα όσο και σε φυσικούς αριθμούς. Στη συνέχεια, θα αναλύσουμε τη διαίρεση των συνηθισμένων κλασμάτων σε δεκαδικά και αντίστροφα, και στο τέλος θα δούμε πώς να διαιρέσουμε σωστά τα κλάσματα που τελειώνουν σε 0, 1, 0, 01, 100, 10 κ.λπ.
Εδώ παίρνουμε μόνο περιπτώσεις με θετικά κλάσματα. Εάν υπάρχει ένα μείον πριν από το κλάσμα, τότε για να ενεργήσετε με αυτό, πρέπει να μελετήσετε το υλικό σχετικά με τη διαίρεση ορθολογικών και πραγματικών αριθμών.
Yandex.RTB R-A-339285-1
Όλα τα δεκαδικά κλάσματα, τόσο πεπερασμένα όσο και περιοδικά, είναι απλώς μια ειδική μορφή γραφής συνηθισμένων κλασμάτων. Επομένως, για αυτά ισχύουν οι ίδιες αρχές όπως και για τα αντίστοιχα συνηθισμένα τους κλάσματα. Έτσι, μειώνουμε την όλη διαδικασία διαίρεσης των δεκαδικών κλασμάτων στην αντικατάστασή τους με συνηθισμένα, ακολουθούμενη από υπολογισμό με μεθόδους που είναι ήδη γνωστές σε εμάς. Ας πάρουμε ένα συγκεκριμένο παράδειγμα.
Παράδειγμα 1
Διαιρέστε το 1,2 με το 0,48.
Λύση
Γράφουμε δεκαδικά κλάσματα με τη μορφή συνηθισμένων κλασμάτων. Θα είμαστε σε θέση να:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Επομένως, πρέπει να διαιρέσουμε το 6 5 με το 12 25 . Πιστεύουμε:
1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2
Από το προκύπτον ακατάλληλο κλάσμα, μπορείτε να επιλέξετε ολόκληρο το μέρος και να πάρετε έναν μικτό αριθμό 2 1 2 ή μπορείτε να το αναπαραστήσετε ως δεκαδικό κλάσμα έτσι ώστε να ταιριάζει με τους αρχικούς αριθμούς: 5 2 \u003d 2, 5. Πώς να το κάνουμε αυτό, έχουμε ήδη γράψει νωρίτερα.
Απάντηση: 1 , 2: 0 , 48 = 2 , 5 .
Παράδειγμα 2
Υπολογίστε πόσα θα είναι 0 , (504) 0 , 56 .
Λύση
Αρχικά, πρέπει να μετατρέψουμε ένα περιοδικό δεκαδικό κλάσμα σε συνηθισμένο.
0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
Μετά από αυτό, θα μεταφράσουμε επίσης το τελικό δεκαδικό κλάσμα σε άλλη μορφή: 0, 56 = 56 100. Τώρα έχουμε δύο αριθμούς με τους οποίους θα είναι εύκολο για εμάς να κάνουμε τους απαραίτητους υπολογισμούς:
0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111
Έχουμε ένα αποτέλεσμα που μπορούμε να το μετατρέψουμε και σε δεκαδικό. Για να το κάνετε αυτό, διαιρέστε τον αριθμητή με τον παρονομαστή χρησιμοποιώντας τη μέθοδο στήλης:
Απάντηση: 0 , (504) : 0 , 56 = 0 , (900) .
Εάν, στο παράδειγμα της διαίρεσης, συναντήσαμε μη περιοδικά δεκαδικά κλάσματα, τότε θα ενεργήσουμε λίγο διαφορετικά. Δεν μπορούμε να τα φέρουμε στα συνηθισμένα συνηθισμένα κλάσματα, οπότε κατά τη διαίρεση, πρέπει πρώτα να τα στρογγυλοποιήσουμε σε ένα συγκεκριμένο ψηφίο. Αυτή η ενέργεια πρέπει να εκτελεστεί τόσο με το μέρισμα όσο και με τον διαιρέτη: θα στρογγυλοποιήσουμε επίσης το υπάρχον πεπερασμένο ή περιοδικό κλάσμα για λόγους ακρίβειας.
Παράδειγμα 3
Βρείτε πόσο θα είναι 0, 779 ... / 1, 5602.
Λύση
Πρώτα απ 'όλα, στρογγυλοποιούμε και τα δύο κλάσματα στα εκατοστά. Έτσι κινούμαστε από άπειρα μη επαναλαμβανόμενα κλάσματα σε πεπερασμένα δεκαδικά:
0 , 779 … ≈ 0 , 78
1 , 5602 ≈ 1 , 56
Μπορούμε να συνεχίσουμε τους υπολογισμούς και να πάρουμε ένα κατά προσέγγιση αποτέλεσμα: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0,5.
Η ακρίβεια του αποτελέσματος θα εξαρτηθεί από τον βαθμό στρογγυλοποίησης.
Απάντηση: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Πώς να διαιρέσετε έναν φυσικό αριθμό με ένα δεκαδικό και αντίστροφα
Η προσέγγιση της διαίρεσης σε αυτή την περίπτωση είναι σχεδόν η ίδια: αντικαθιστούμε πεπερασμένα και περιοδικά κλάσματα με συνηθισμένα και στρογγυλοποιούμε άπειρα μη περιοδικά. Ας ξεκινήσουμε με το παράδειγμα της διαίρεσης με φυσικό αριθμό και δεκαδικό κλάσμα.
Παράδειγμα 4
Διαιρέστε το 2,5 με το 45.
Λύση
Ας φέρουμε το 2, 5 στη μορφή ενός συνηθισμένου κλάσματος: 255 10 \u003d 51 2. Στη συνέχεια, πρέπει απλώς να το διαιρέσουμε με έναν φυσικό αριθμό. Ξέρουμε ήδη πώς να το κάνουμε αυτό:
25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30
Αν μεταφράσουμε το αποτέλεσμα σε δεκαδικό συμβολισμό, τότε παίρνουμε 0 , 5 (6) .
Απάντηση: 25 , 5: 45 = 0 , 5 (6) .
Η μέθοδος διαίρεσης με στήλη είναι καλή όχι μόνο για φυσικούς αριθμούς. Κατ' αναλογία, μπορούμε να το χρησιμοποιήσουμε και για κλάσματα. Παρακάτω θα αναφέρουμε τη σειρά των ενεργειών που πρέπει να πραγματοποιηθούν για αυτό.
Ορισμός 1
Για να διαιρέσετε μια στήλη δεκαδικών κλασμάτων με φυσικούς αριθμούς, πρέπει:
1. Προσθέστε μερικά μηδενικά στο δεκαδικό κλάσμα στα δεξιά (για διαίρεση, μπορούμε να προσθέσουμε όποιον αριθμό από αυτά χρειαζόμαστε).
2. Διαιρέστε ένα δεκαδικό κλάσμα με έναν φυσικό αριθμό χρησιμοποιώντας έναν αλγόριθμο. Όταν τελειώσει η διαίρεση του ακέραιου μέρους του κλάσματος, βάζουμε κόμμα στο πηλίκο που προκύπτει και μετράμε περαιτέρω.
Το αποτέλεσμα μιας τέτοιας διαίρεσης μπορεί να είναι είτε ένα πεπερασμένο είτε ένα άπειρο περιοδικό δεκαδικό κλάσμα. Εξαρτάται από το υπόλοιπο: αν είναι μηδέν, τότε το αποτέλεσμα θα είναι πεπερασμένο και αν τα υπόλοιπα αρχίσουν να επαναλαμβάνονται, τότε η απάντηση θα είναι ένα περιοδικό κλάσμα.
Ας πάρουμε μερικές εργασίες ως παράδειγμα και ας προσπαθήσουμε να ολοκληρώσουμε αυτά τα βήματα ήδη με συγκεκριμένους αριθμούς.
Παράδειγμα 5
Υπολογίστε πόσο θα είναι 65 , 14 4 .
Λύση
Χρησιμοποιούμε τη μέθοδο στήλης. Για να το κάνετε αυτό, προσθέστε δύο μηδενικά στο κλάσμα και λάβετε το δεκαδικό κλάσμα 65, 1400, το οποίο θα είναι ίσο με το αρχικό. Τώρα γράφουμε μια στήλη για διαίρεση με 4:

Ο αριθμός που προκύπτει θα είναι το αποτέλεσμα της διαίρεσης του ακέραιου μέρους που χρειαζόμαστε. Βάζουμε κόμμα, χωρίζοντας το και συνεχίζουμε:

Φτάσαμε στο μηδέν υπόλοιπο, επομένως, η διαδικασία διαίρεσης ολοκληρώθηκε.
Απάντηση: 65 , 14: 4 = 16 , 285 .
Παράδειγμα 6
Διαιρέστε το 164,5 με το 27.
Λύση
Διαιρούμε πρώτα το κλασματικό μέρος και παίρνουμε:
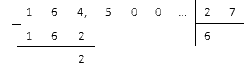
Διαχωρίζουμε το σχήμα που προκύπτει με κόμμα και συνεχίζουμε να διαιρούμε:

Βλέπουμε ότι τα υπόλοιπα άρχισαν να επαναλαμβάνονται περιοδικά και οι αριθμοί εννέα, δύο και πέντε άρχισαν να εναλλάσσονται στο πηλίκο. Θα σταματήσουμε εκεί και θα γράψουμε την απάντηση ως περιοδικό κλάσμα 6, 0 (925) .
Απάντηση: 164 , 5: 27 = 6 , 0 (925) .
Μια τέτοια διαίρεση μπορεί να περιοριστεί στη διαδικασία εύρεσης ενός ιδιωτικού δεκαδικού κλάσματος και ενός φυσικού αριθμού που ήδη περιγράφηκε παραπάνω. Για να γίνει αυτό, πρέπει να πολλαπλασιάσουμε το μέρισμα και τον διαιρέτη με 10, 100 κ.λπ. έτσι ώστε ο διαιρέτης να μετατραπεί σε φυσικό αριθμό. Στη συνέχεια εκτελούμε την παραπάνω σειρά ενεργειών. Αυτή η προσέγγιση είναι δυνατή λόγω των ιδιοτήτων της διαίρεσης και του πολλαπλασιασμού. Σε κυριολεκτική μορφή, τα γράψαμε ως εξής:
a: b = (a 10) : (b 10) , a: b = (a 100) : (b 100) και ούτω καθεξής.
Ας διατυπώσουμε τον κανόνα:
Ορισμός 2
Για να διαιρέσετε ένα τελικό δεκαδικό κλάσμα με ένα άλλο, πρέπει:
1. Μετακινήστε το κόμμα στο μέρισμα και το διαιρέτη προς τα δεξιά με τον αριθμό των χαρακτήρων που είναι απαραίτητοι για να μετατρέψετε τον διαιρέτη σε φυσικό αριθμό. Εάν δεν υπάρχουν αρκετά σημάδια στο μέρισμα, προσθέτουμε μηδενικά σε αυτό στη δεξιά πλευρά.
2. Μετά από αυτό, διαιρούμε το κλάσμα με μια στήλη με τον φυσικό αριθμό που προκύπτει.
Ας ρίξουμε μια ματιά σε ένα συγκεκριμένο πρόβλημα.
Παράδειγμα 7
Διαιρέστε το 7, 287 με το 2, 1.
Λύση: Για να κάνουμε τον διαιρέτη φυσικό αριθμό, πρέπει να μετακινήσουμε το κόμμα με έναν χαρακτήρα προς τα δεξιά. Έτσι προχωρήσαμε στη διαίρεση του δεκαδικού κλάσματος 72, 87 με 21. Ας γράψουμε τους αριθμούς που προέκυψαν σε μια στήλη και ας υπολογίσουμε

Απάντηση: 7 , 287: 2 , 1 = 3 , 47
Παράδειγμα 8
Υπολογίστε 16 , 3 0 , 021 .
Λύση
Θα πρέπει να μετακινήσουμε το κόμμα σε τρία ψηφία. Δεν υπάρχουν αρκετά ψηφία στον διαιρέτη για αυτό, πράγμα που σημαίνει ότι πρέπει να χρησιμοποιήσετε επιπλέον μηδενικά. Πιστεύουμε ότι το τελικό αποτέλεσμα θα είναι:

Βλέπουμε την περιοδική επανάληψη των υπολειμμάτων 4 , 19 , 1 , 10 , 16 , 13 . Το πηλίκο επαναλαμβάνει 1 , 9 , 0 , 4 , 7 και 5 . Τότε το αποτέλεσμά μας είναι το περιοδικό δεκαδικό 776 , (190476) .
Απάντηση: 16 , 3: 0 , 021 = 776 , (190476)
Η μέθοδος που περιγράφεται από εμάς σας επιτρέπει να κάνετε το αντίθετο, δηλαδή να διαιρέσετε έναν φυσικό αριθμό με ένα τελικό δεκαδικό κλάσμα. Ας δούμε πώς γίνεται.
Παράδειγμα 9
Υπολογίστε πόσα θα είναι 3 5 , 4 .
Λύση
Προφανώς, θα πρέπει να μετακινήσουμε το κόμμα προς τα δεξιά κατά έναν χαρακτήρα. Μετά από αυτό μπορούμε να αρχίσουμε να διαιρούμε το 30, το 0 με το 54. Ας γράψουμε τα δεδομένα σε μια στήλη και ας υπολογίσουμε το αποτέλεσμα:
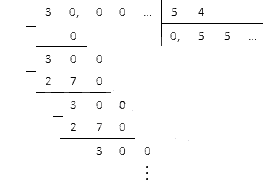
Η επανάληψη του υπολοίπου μας δίνει τον αριθμό 0 , (5) , που είναι περιοδικό δεκαδικό.
Απάντηση: 3: 5 , 4 = 0 , (5) .
Πώς να διαιρέσετε τα δεκαδικά με 1000, 100, 10 κ.λπ.
Σύμφωνα με τους ήδη μελετημένους κανόνες για τη διαίρεση συνηθισμένων κλασμάτων, η διαίρεση ενός κλάσματος σε δεκάδες, εκατοντάδες, χιλιάδες είναι παρόμοια με τον πολλαπλασιασμό του επί 1/1000, 1/100, 1/10 κ.λπ. Αποδεικνύεται ότι για να γίνει η διαίρεση , σε αυτήν την περίπτωση, αρκεί απλώς να μετακινήσετε το κόμμα στα ψηφία του επιθυμητού ποσού. Εάν δεν υπάρχουν αρκετές τιμές στον αριθμό για μεταφορά, πρέπει να προσθέσετε τον απαιτούμενο αριθμό μηδενικών.
Παράδειγμα 10
Άρα, 56, 21: 10 = 5, 621 και 0, 32: 100.000 = 0, 0000032.
Στην περίπτωση των άπειρων δεκαδικών, κάνουμε το ίδιο.
Παράδειγμα 11
Για παράδειγμα, 3 , (56) : 1000 = 0 , 003 (56) και 593 , 374 ... : 100 = 5 , 93374 ... .
Πώς να διαιρέσετε τα δεκαδικά με 0,001, 0,01, 0,1 κ.λπ.
Χρησιμοποιώντας τον ίδιο κανόνα, μπορούμε επίσης να διαιρέσουμε τα κλάσματα με τις καθορισμένες τιμές. Αυτή η ενέργεια θα είναι παρόμοια με τον πολλαπλασιασμό με 1000 , 100 , 10 αντίστοιχα. Για να γίνει αυτό, μετακινούμε το κόμμα σε ένα, δύο ή τρία ψηφία, ανάλογα με τις συνθήκες του προβλήματος, και προσθέτουμε μηδενικά εάν δεν υπάρχουν αρκετά ψηφία στον αριθμό.
Παράδειγμα 12
Για παράδειγμα, 5, 739: 0, 1 = 57, 39 και 0, 21: 0, 00001 = 21.000.
Αυτός ο κανόνας ισχύει και για άπειρα δεκαδικά. Σας συμβουλεύουμε μόνο να είστε προσεκτικοί με την περίοδο του κλάσματος που προκύπτει στην απάντηση.
Άρα, 7 , 5 (716) : 0 , 01 = 757 , (167) , γιατί αφού μετακινήσαμε το κόμμα στον δεκαδικό συμβολισμό 7 , 5716716716 ... δύο ψηφία προς τα δεξιά, πήραμε 757 , 167167 ... .
Αν έχουμε μη περιοδικά κλάσματα στο παράδειγμα, τότε όλα είναι πιο απλά: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... .
Πώς να διαιρέσετε έναν μικτό αριθμό ή ένα κοινό κλάσμα με ένα δεκαδικό και αντίστροφα
Μειώνουμε επίσης αυτή την ενέργεια σε πράξεις με συνηθισμένα κλάσματα. Για να το κάνετε αυτό, αντικαταστήστε τους δεκαδικούς αριθμούς με τα αντίστοιχα συνηθισμένα κλάσματα και γράψτε τον μικτό αριθμό ως ακατάλληλο κλάσμα.
Αν διαιρέσουμε ένα μη περιοδικό κλάσμα με έναν συνηθισμένο ή μεικτό αριθμό, πρέπει να κάνουμε το αντίθετο, αντικαθιστώντας το συνηθισμένο κλάσμα ή μεικτό αριθμό με το αντίστοιχο δεκαδικό κλάσμα.
Εάν παρατηρήσετε κάποιο λάθος στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
